Trig 00-02: Tau
It’s true. The circle constant has been defined incorrectly. If you’d like to see all the reasons why, head over to the Tau Manifesto.
If you made it through the last lesson on radians, you saw first-hand how quickly pi becomes unwieldy. Let’s take a look at how we got here.
One of the special features of a circle is that the width of the shape is constant. We can measure a circle from any point and the distance from one side to the opposite side is always the same.
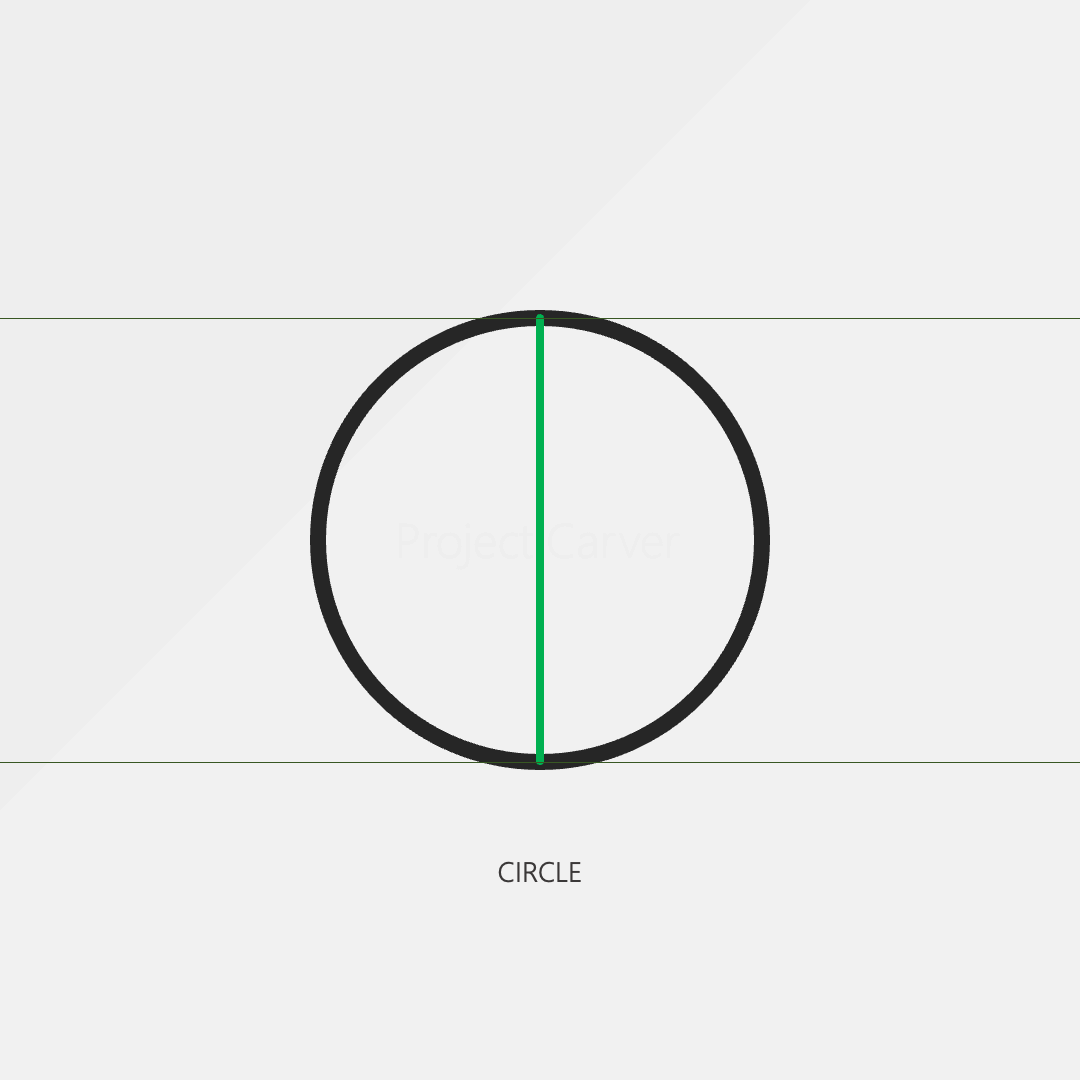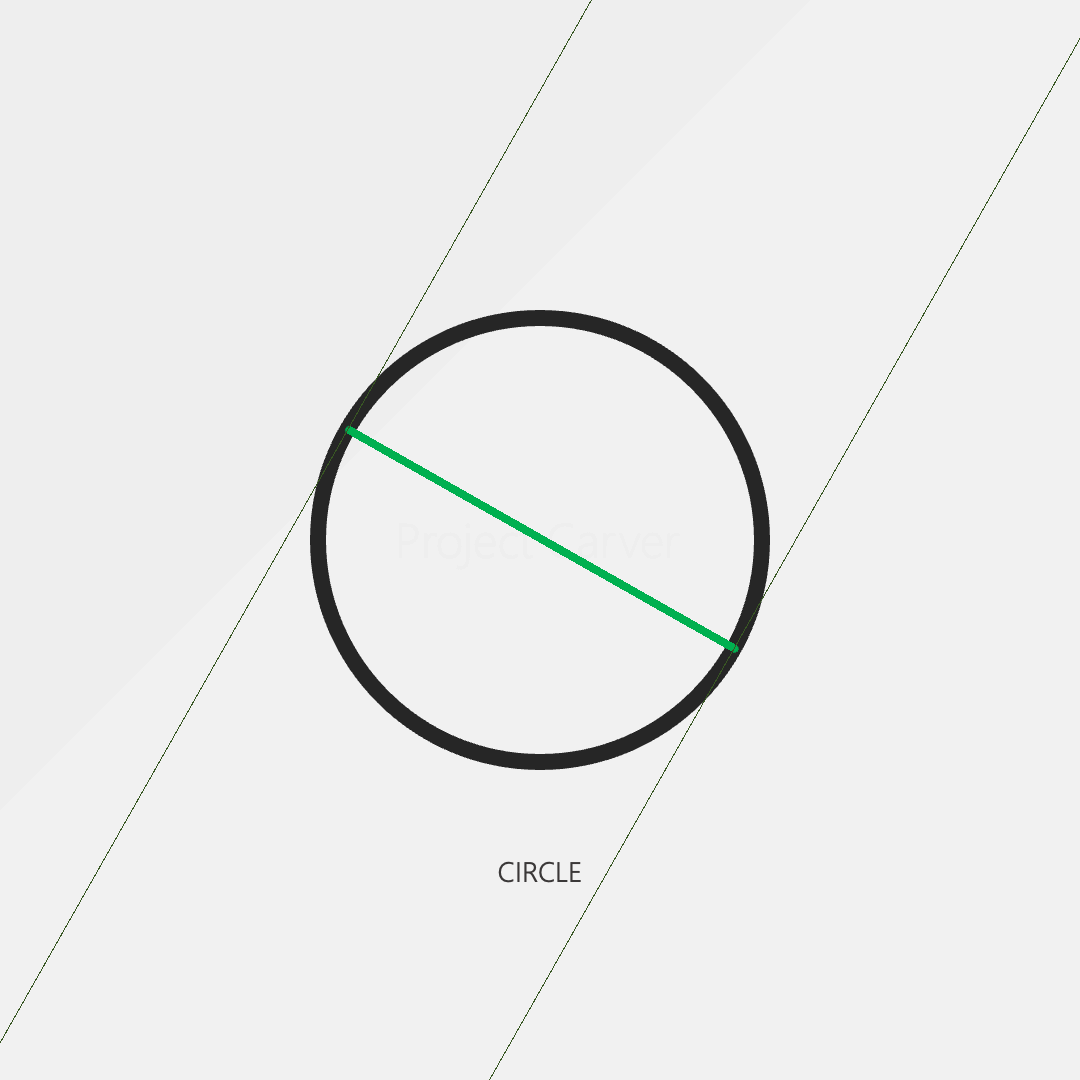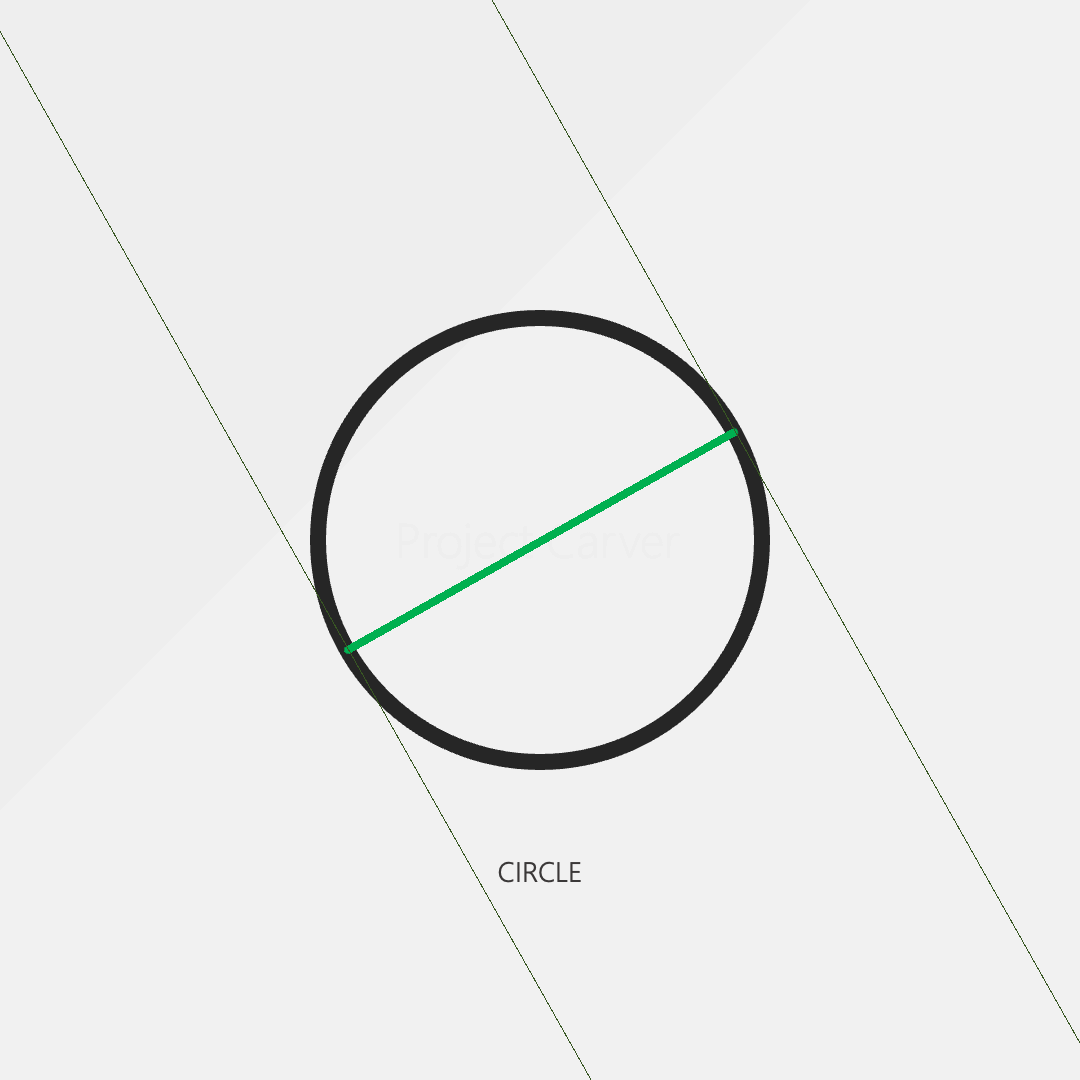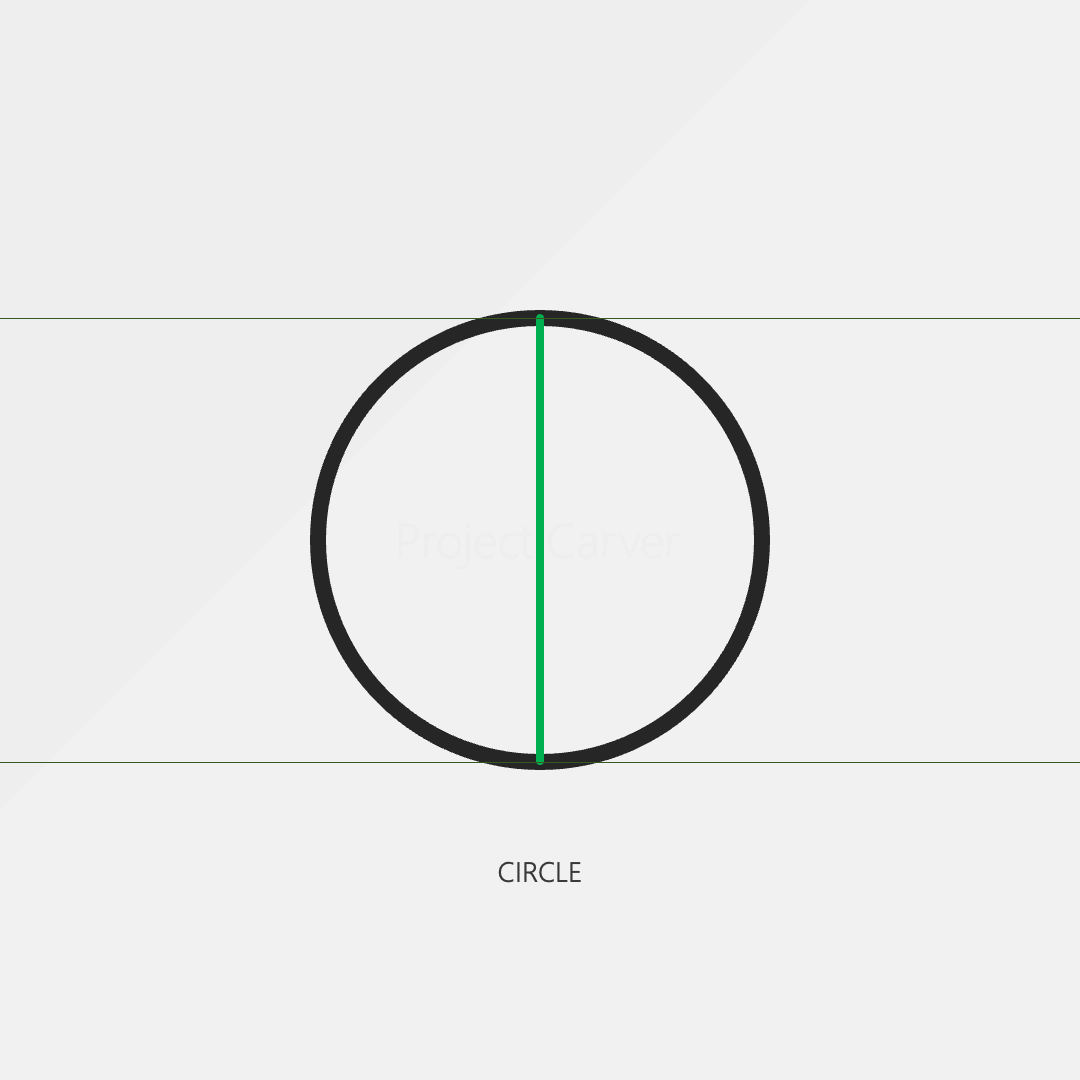

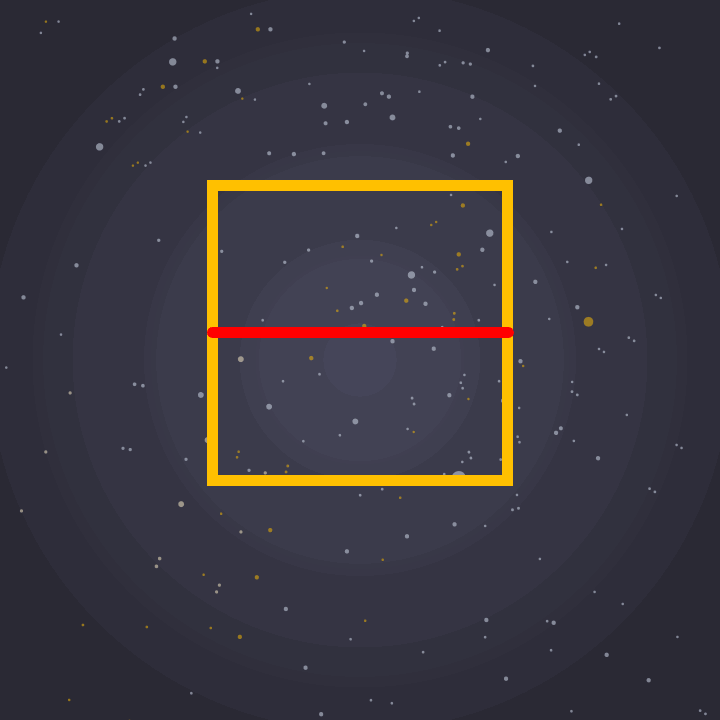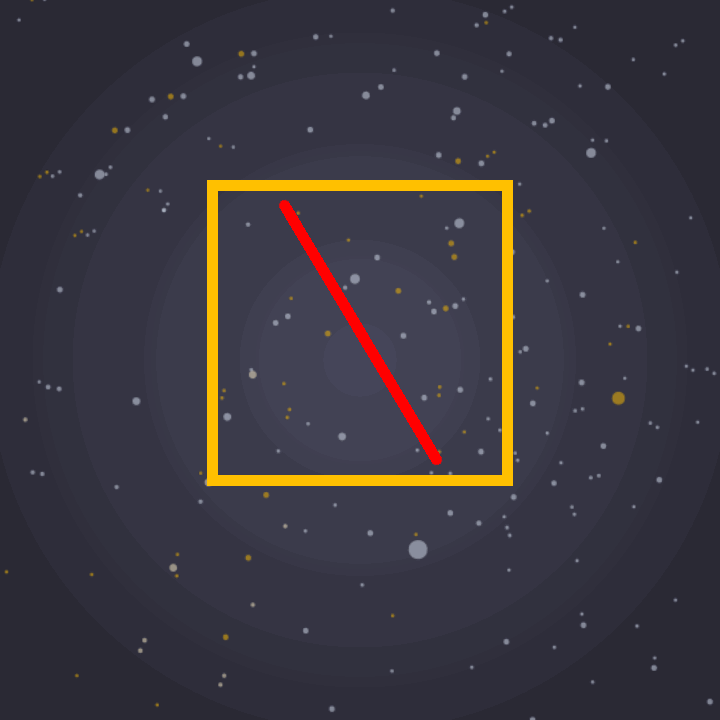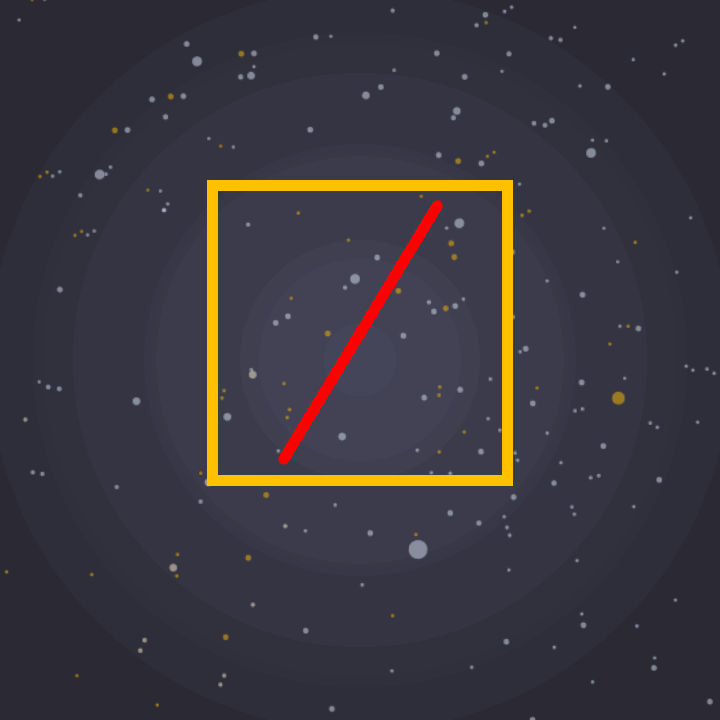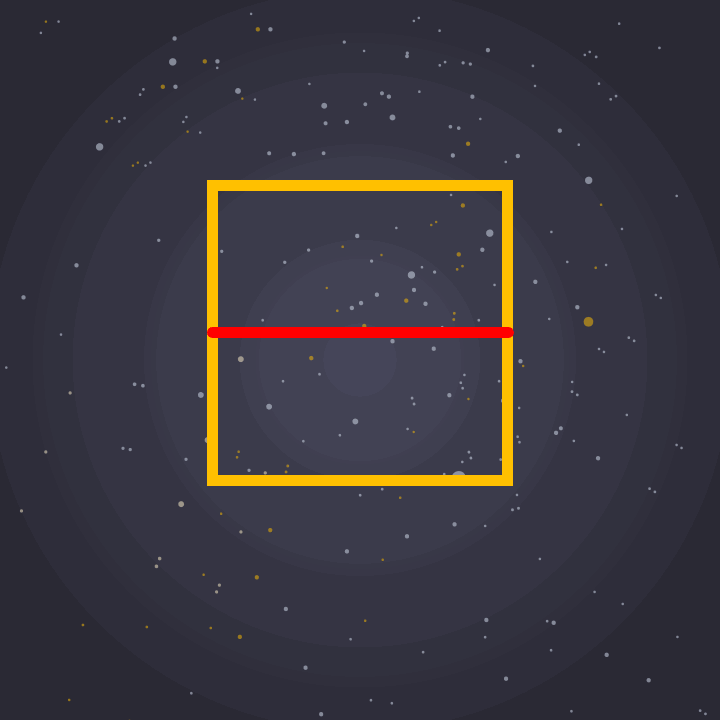

However, the circle isn’t the only shape with this property. The reuleaux triangle shown below is one of many shapes that also have a constant width.
YouTube Search: constant-width shapes
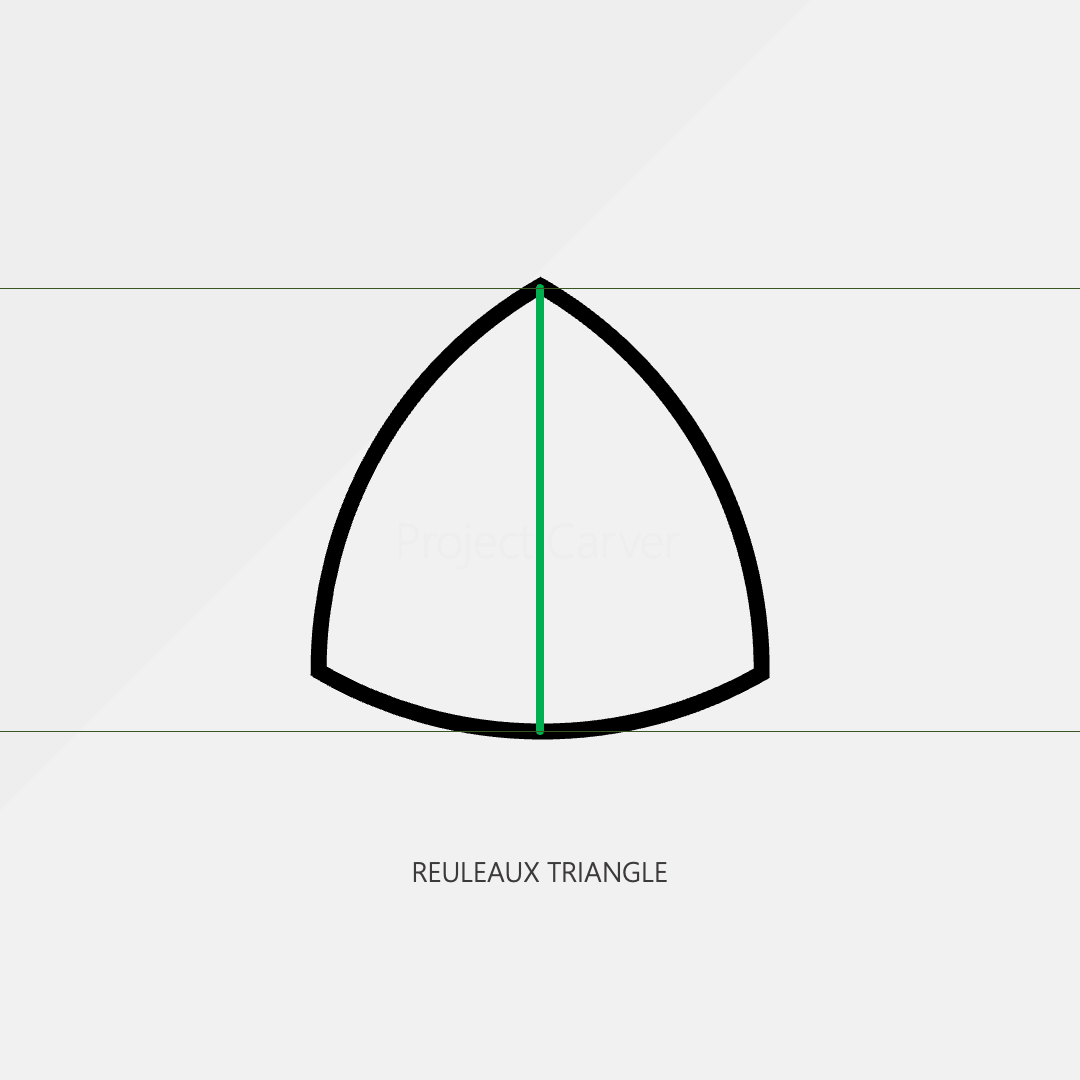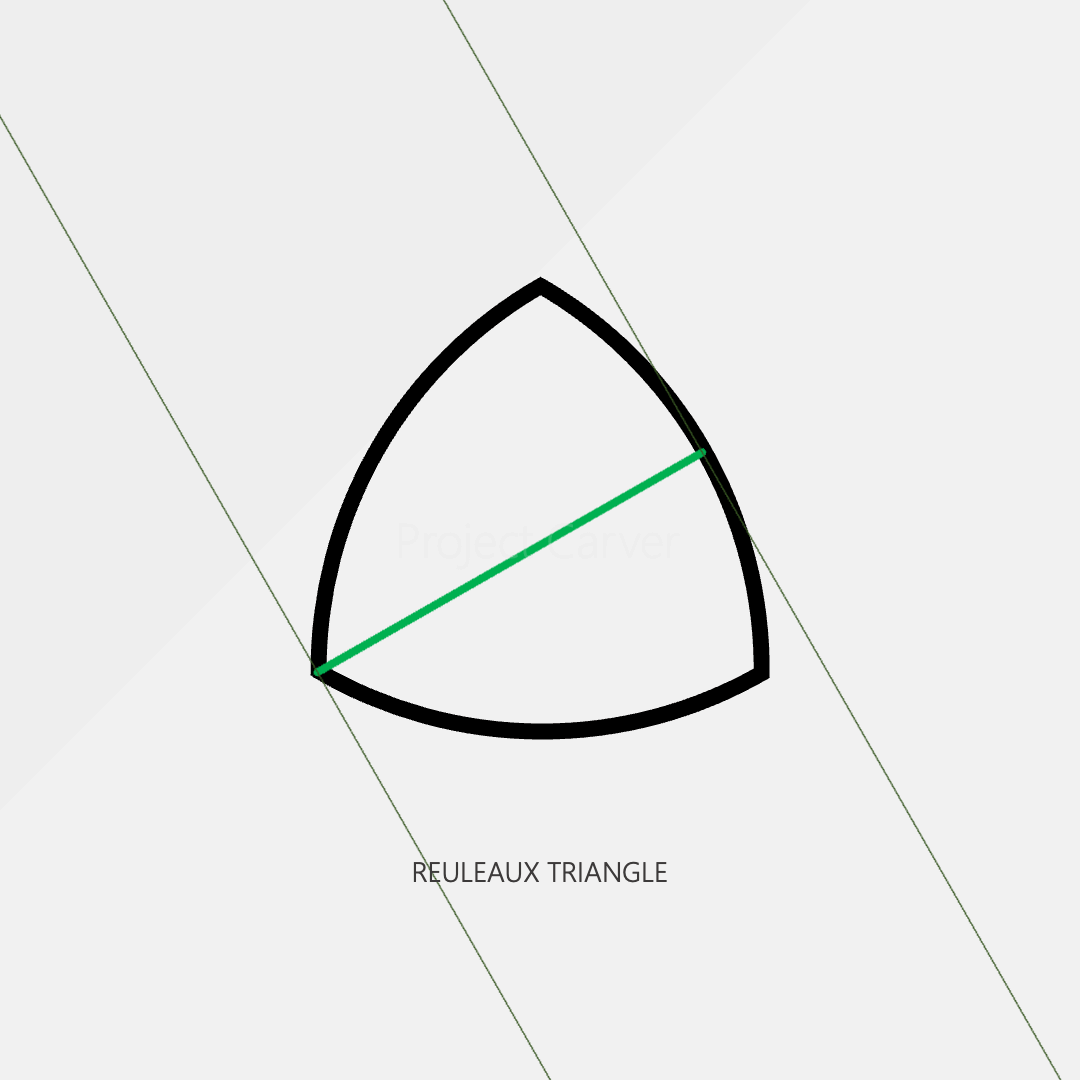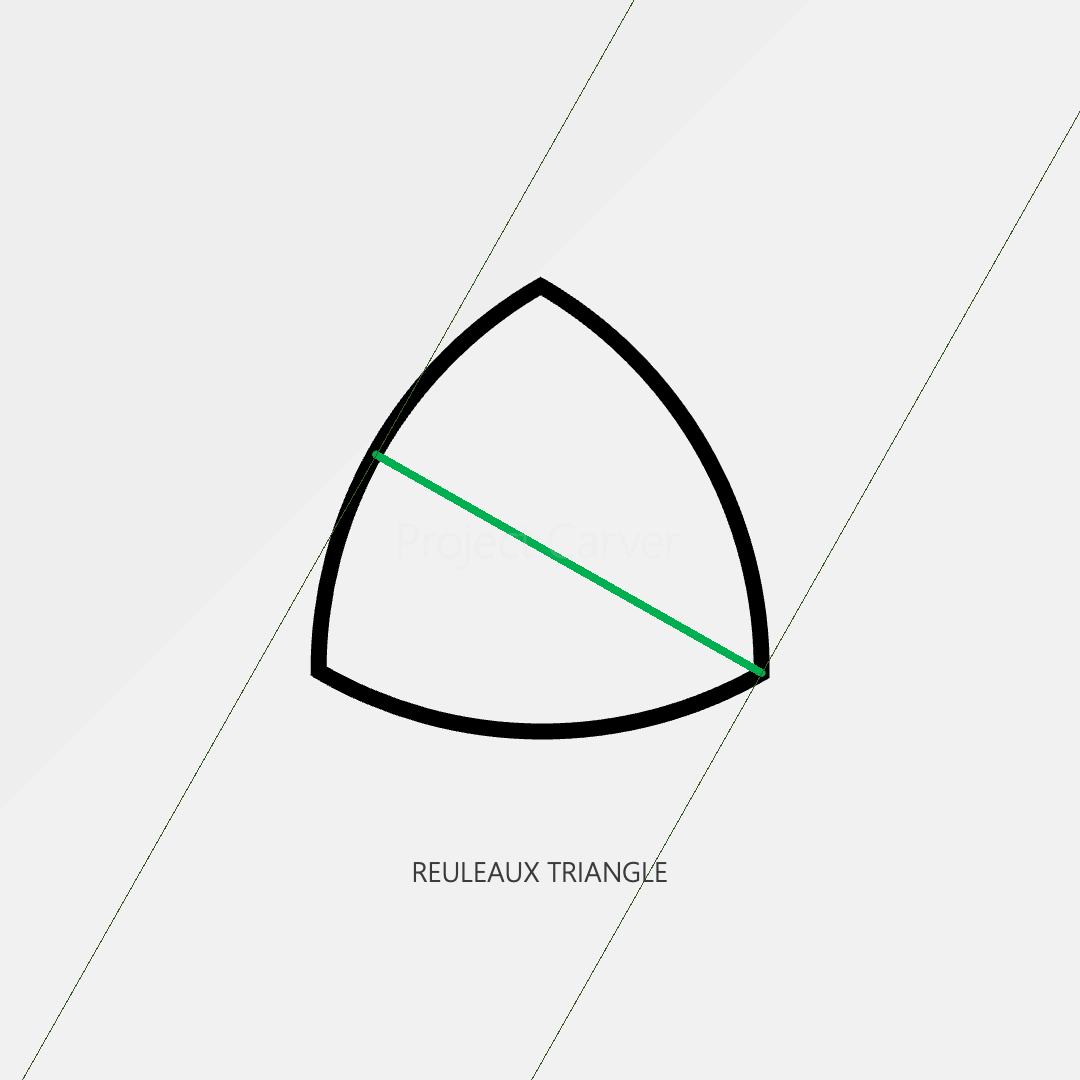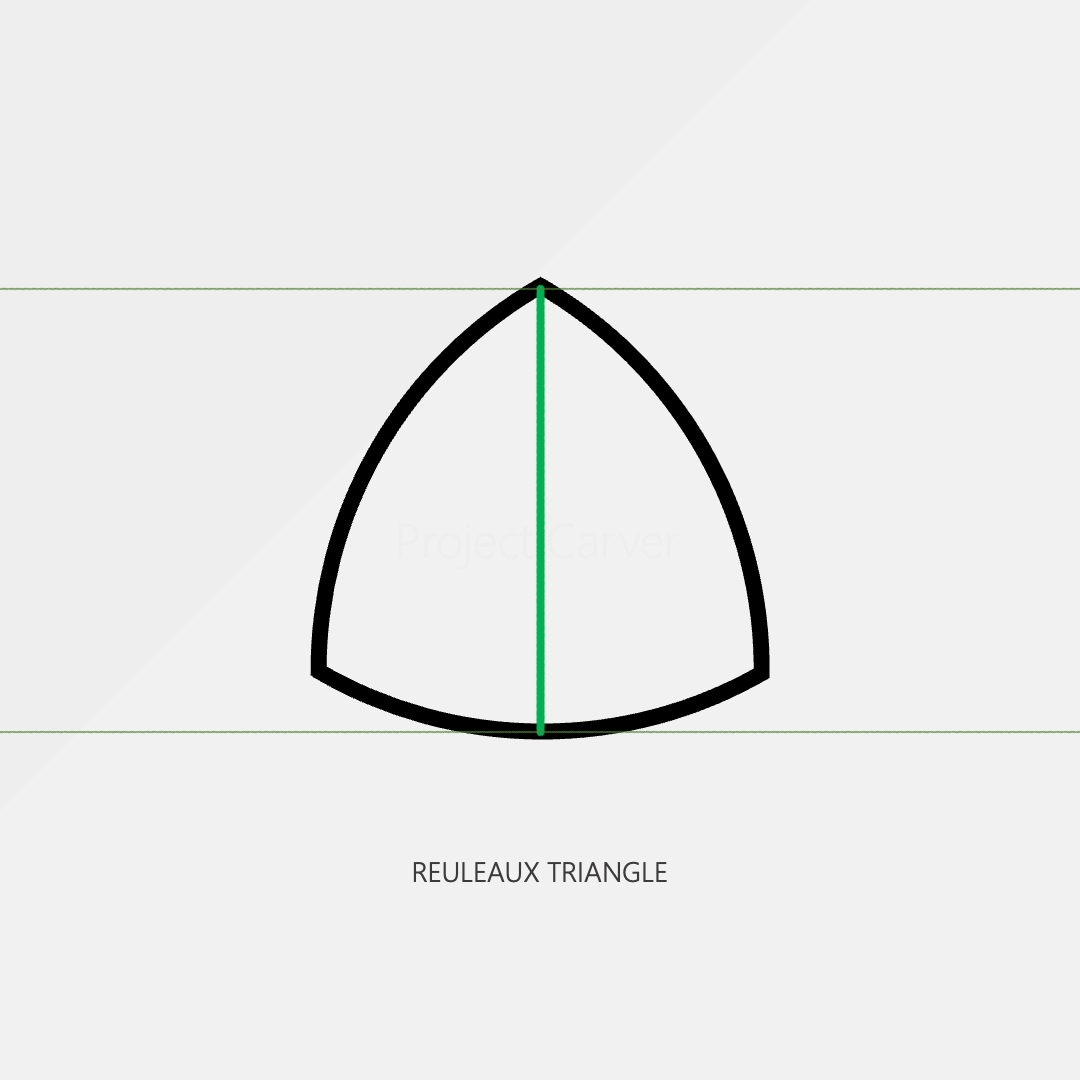
So right away, we know that when defining a circle constant it should be connected to what makes a circle unique, its constant radius.
The Circle™ : the only constant-radius 2D shape in the universe
So how is pi currently defined? Let’s say we would like to build something in a circular shape. How about a fence with width 1m? The question is: how much material would we need to build this fence?

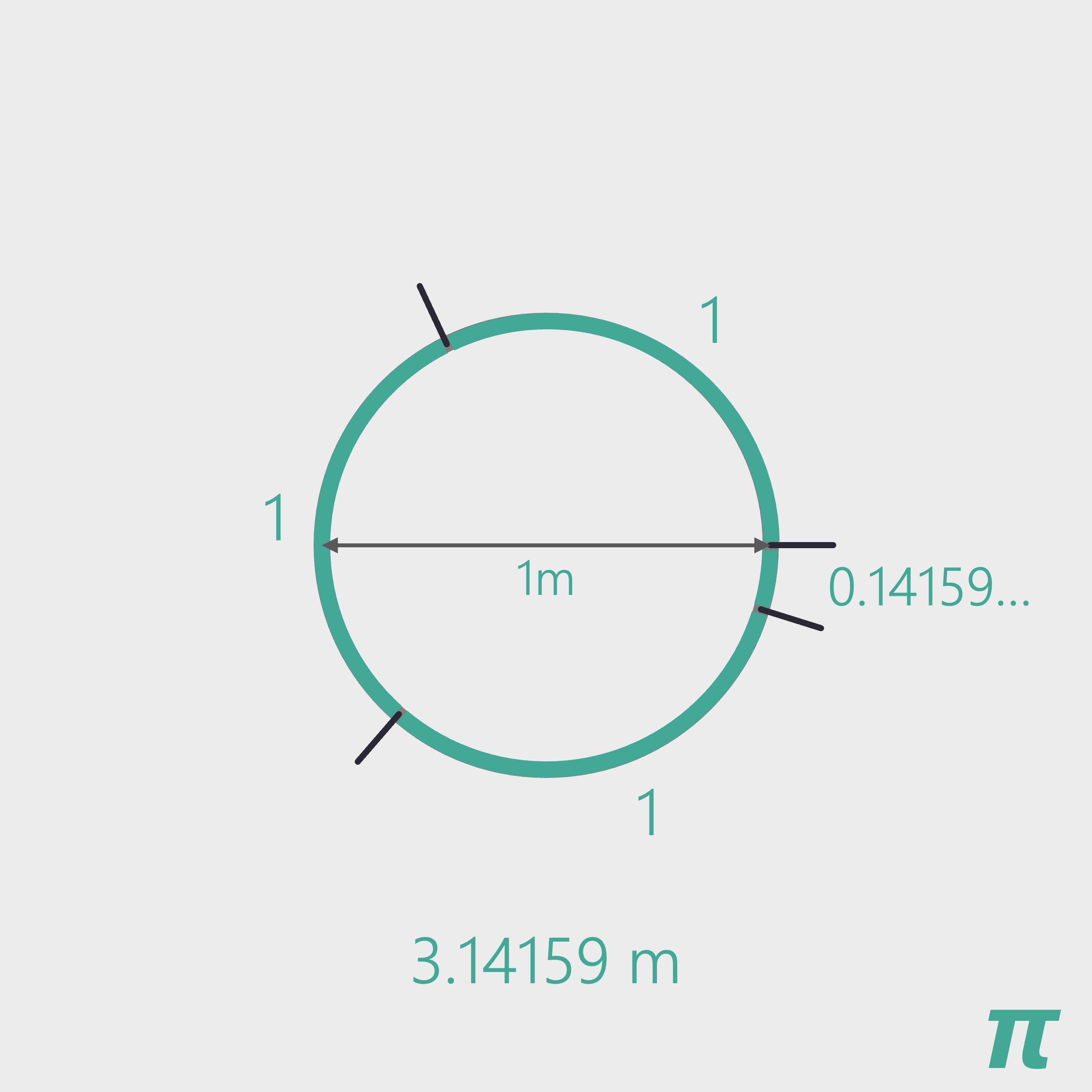

It turns out that for any circle, if the width is known, the perimeter is always about 3 times as large. Specifically, its 3.14159… times as large. Or pi times as large as the width.
Note
The story of how humans discovered pi and defined it to further and further precision is an interesting story in and of itself. One of these chapters of development is covered in Veritasium’s The Discovery That Change Pi.
Let’s say we want to construct a circle of width 5m. Just multiply the width by pi and we have our perimeter.




As we can see, pi is pretty useful when applied in this context. And for 99.9% of applications, we usually think in this way. We would like to construct a circle. We know the width. We can then use pi to find the perimeter or circumference of the circle.
Alright, let’s see what things would look like if we instead used our radius (half of the width).

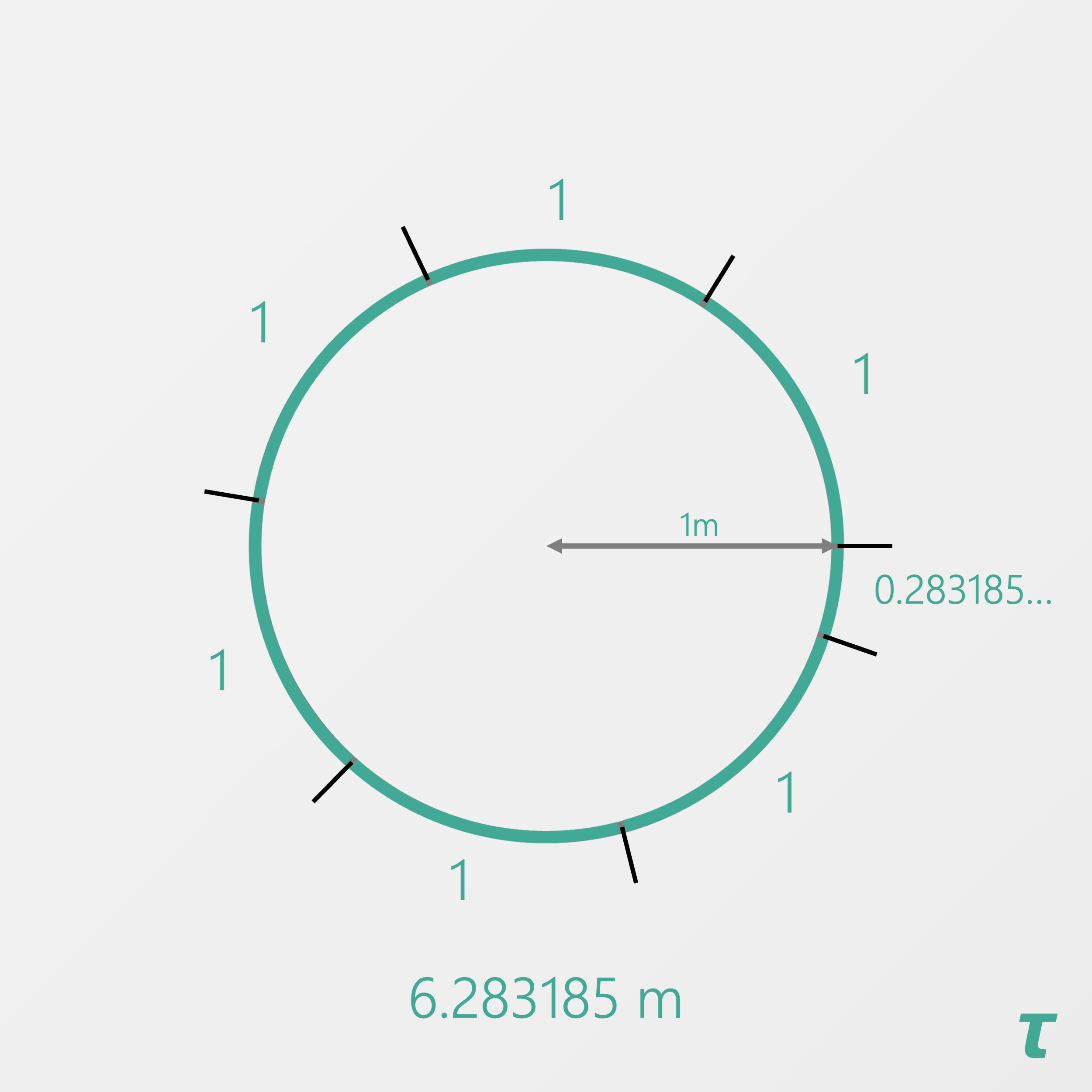


Looks pretty familiar, right? It turns out that if we know the radius (half the width) of the circle, the perimeter is about 6 times as large. 6.283185… times as large to be exact. This is tau.




And once again, if we change the radius to 5m, then the perimeter or circumference is about 6 times as big. Or tau times as big.
So we see that by either definition we still come to the same result. We can find the perimeter from the width or from the radius (half-width).
And so we arrive at our question:
Should the circle constant be defined as
3.141593…
or
6.283185…
?
Argument for 3.141593
It’s more human-friendly like Fahrenheit, Degrees, and Feet. For constructing circles, it’s our constant of choice.
Argument for 6.283185
It’s more circle friendly. It defines the circle constant true to its meaning. It’s more math friendly and makes calculations easier and simpler (see below).
Ok, so remember radians and how awkward they were to learn? Let’s revisit that topic and see how much easier it would be with our new circle constant, tau.
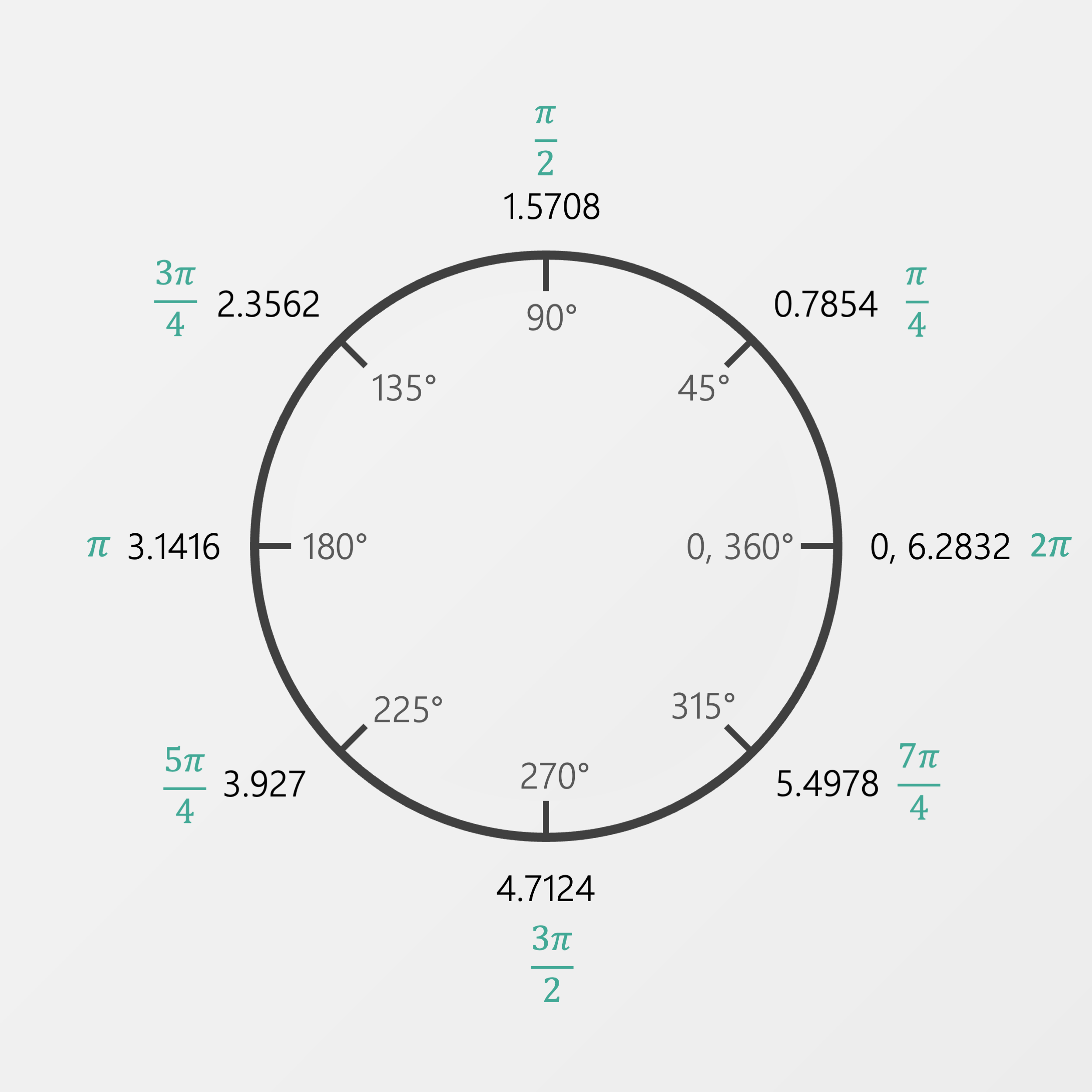
Remember this diagram from the last lesson?
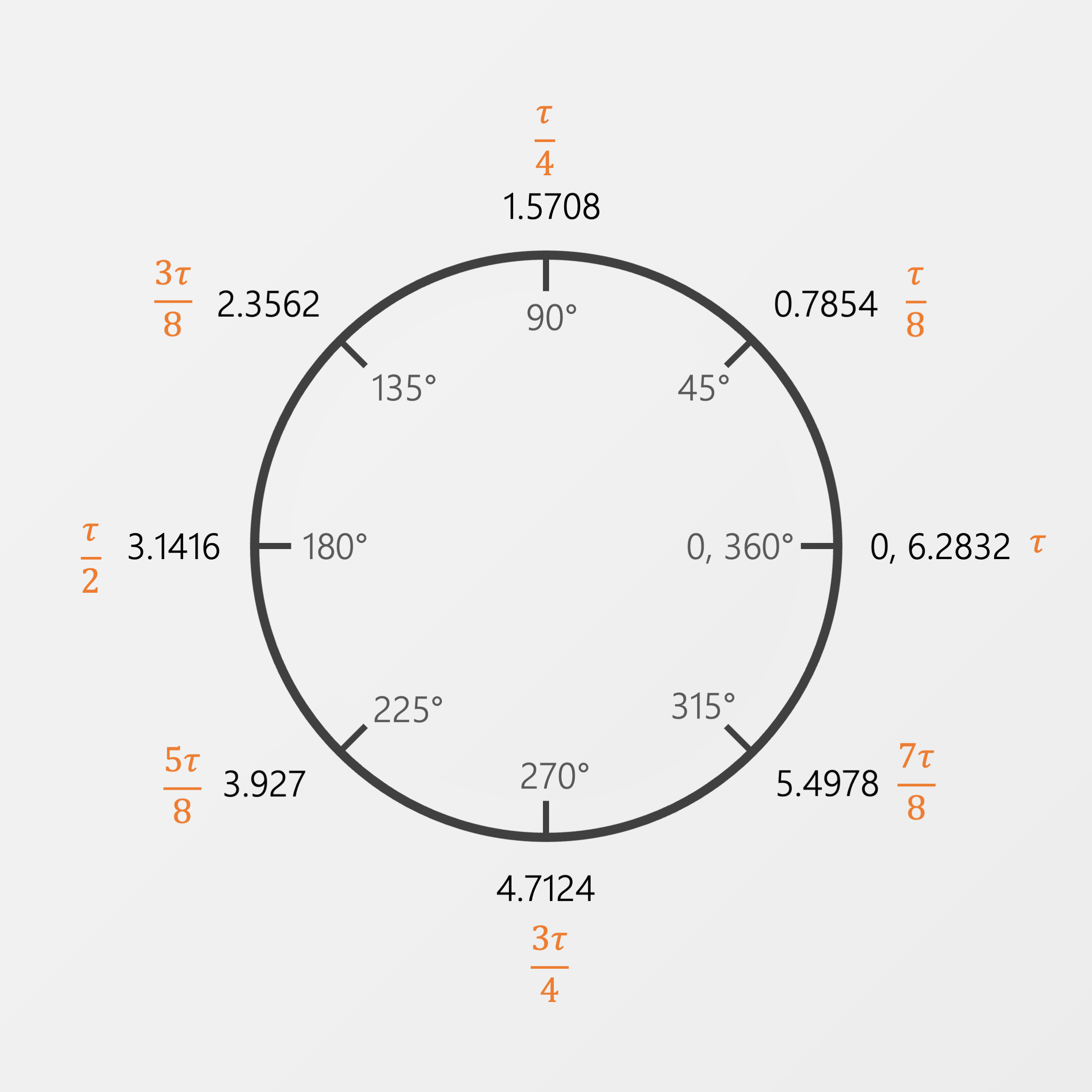
Replacing pi with the new constant of tau, we get this:
Isn’t that so much easier to think about? A quarter turn is just a quarter tau. A half turn is just half of tau.
And this isn’t the only place where tau works better. If you’re interested in seeing plenty more examples, head over to the Tau Manifesto.
Note
Tau hasn’t seen widespread adoption like pi has. So while we will use tau for the rest of the unit on trig, we will also continue to use pi to make sure our math works in the classroom as well.
Ok, one last thing. We’ve established that tau and radians go together like peanut butter and jelly.
One of the questions that might have come up for you during these last two lessons is, what about creating an angle system based on the diameter of a circle?
In keeping with our practice of making up new math, we present the Diamerian (die-uh-meer-ee-an). Does this system have any uses compared with a radian? Any advantages? Disadvantages?
To answer these questions and see just how special a radian is, we have to discuss turns. On to the next lesson.