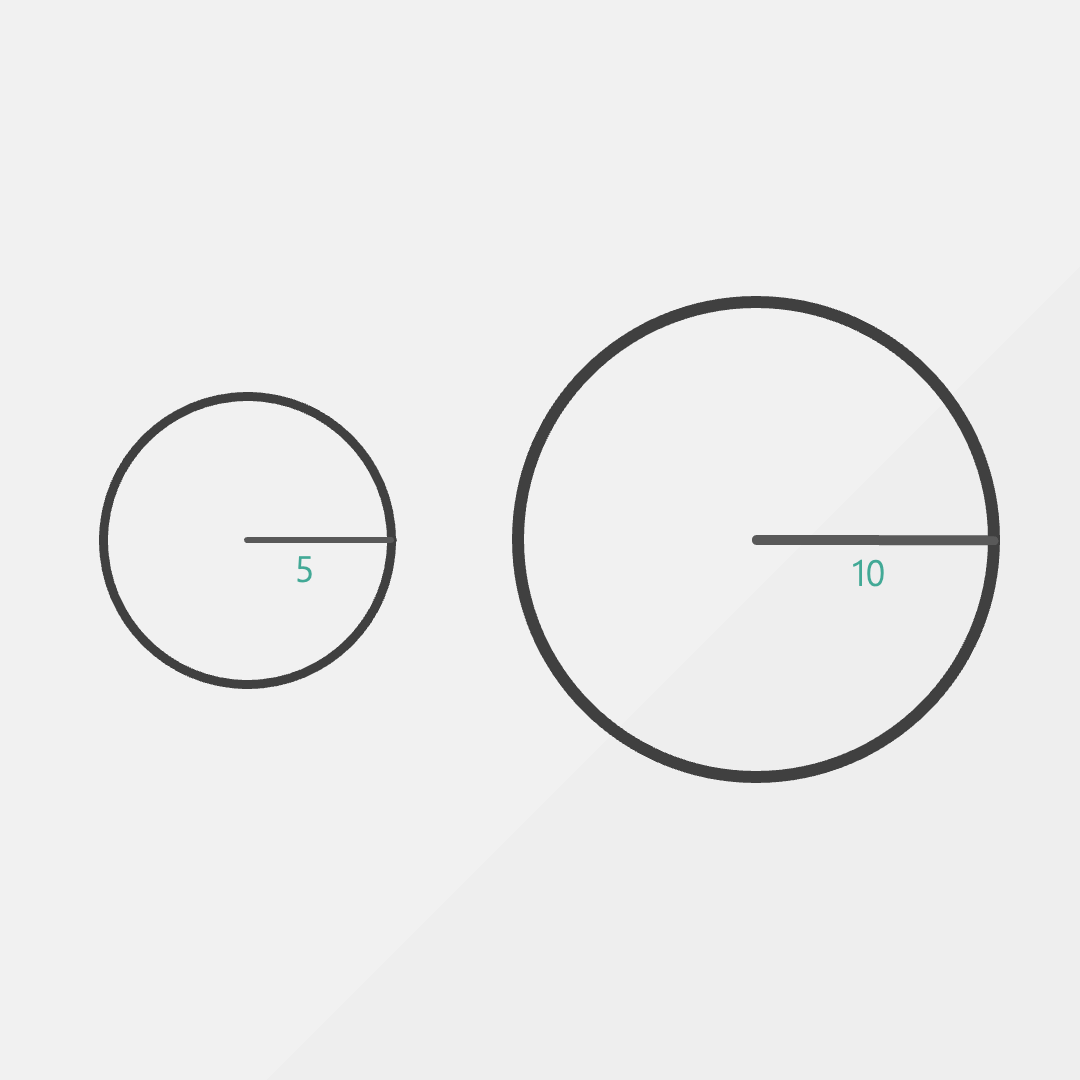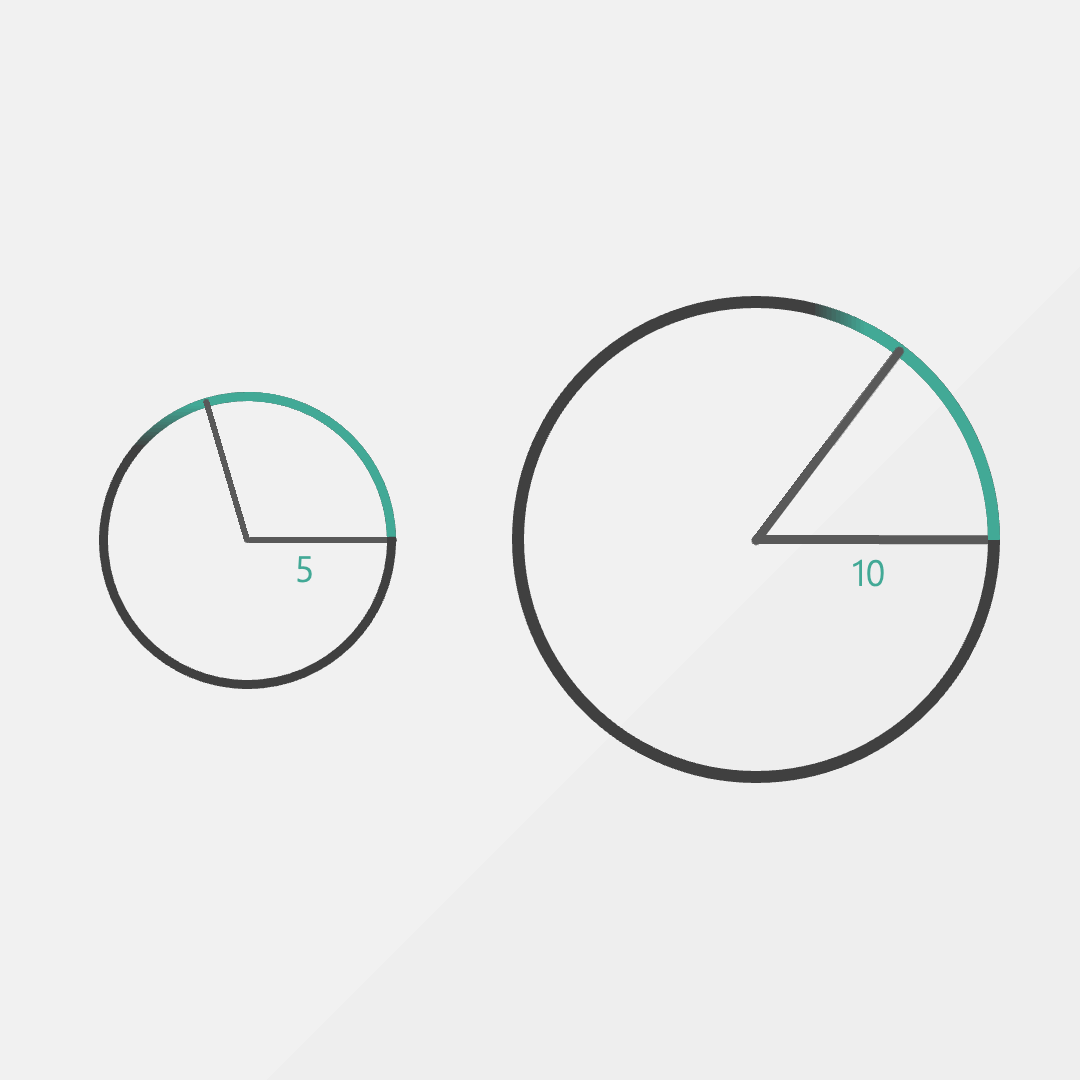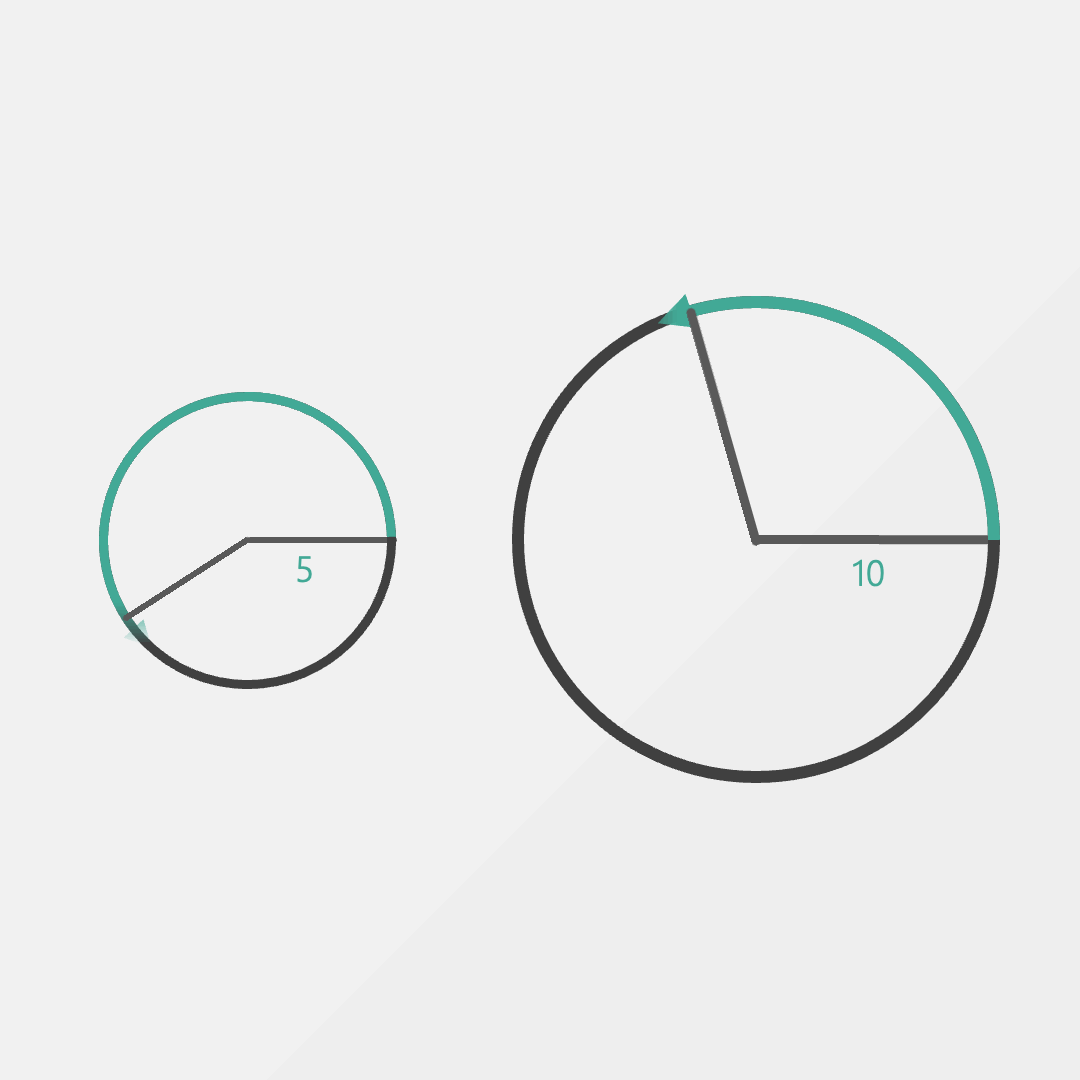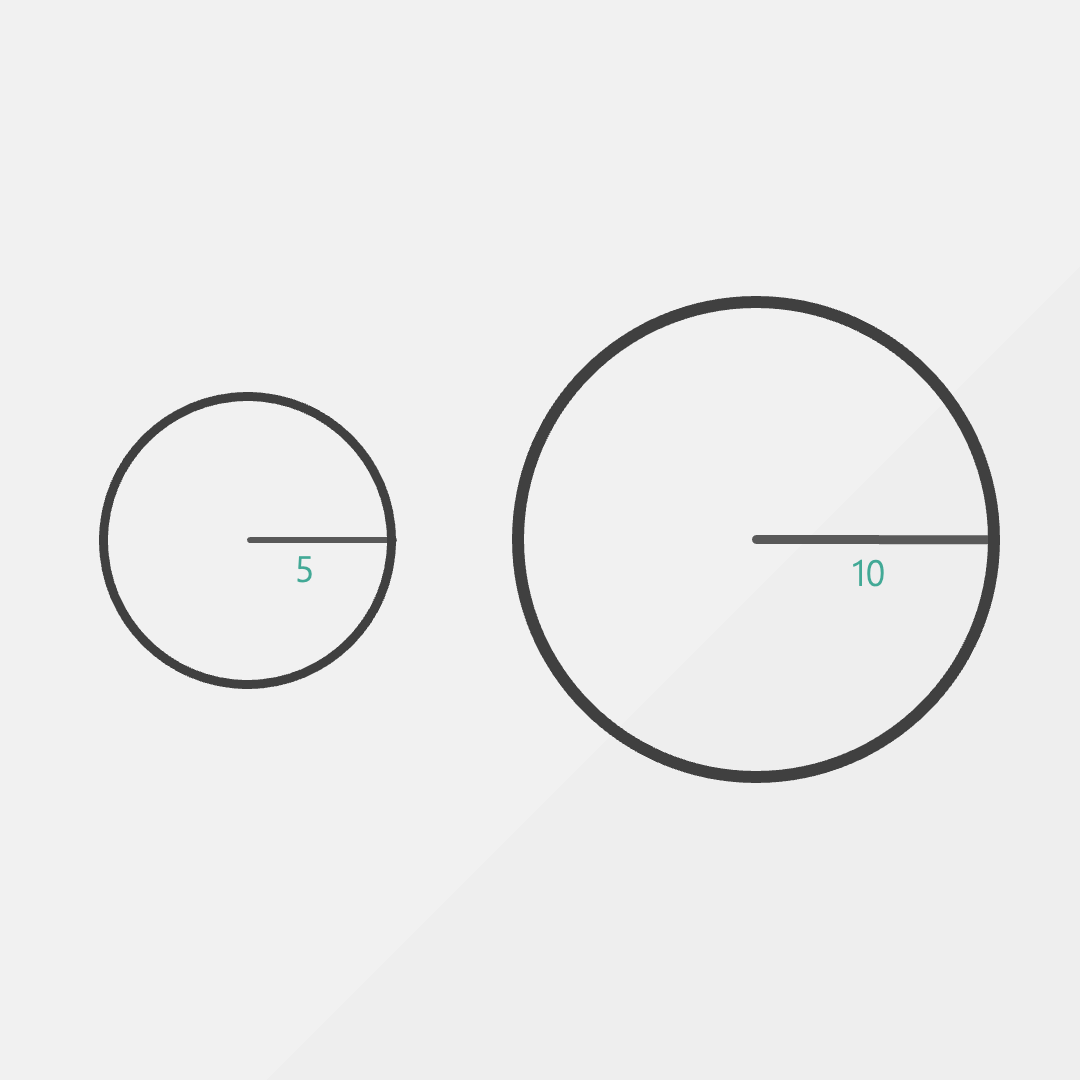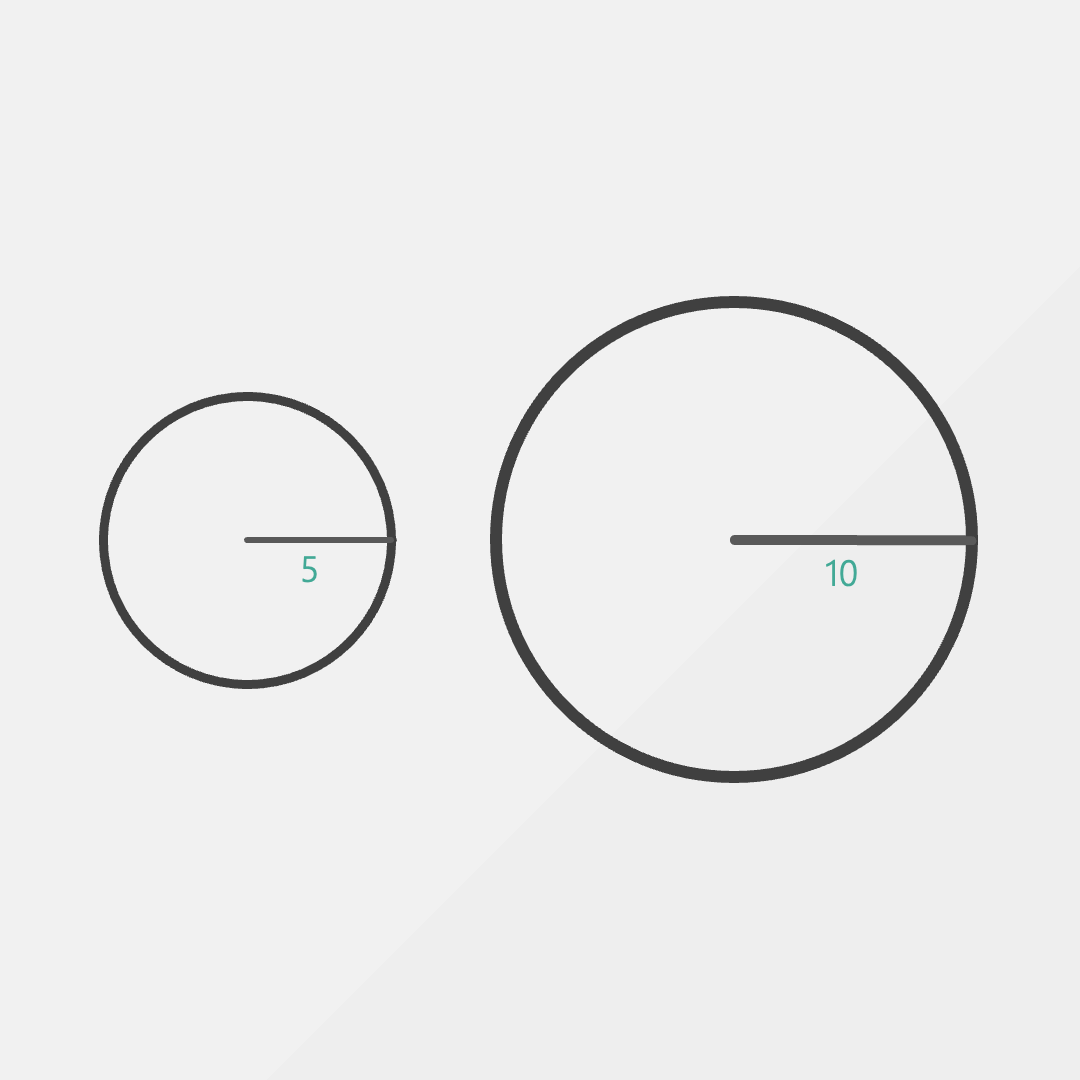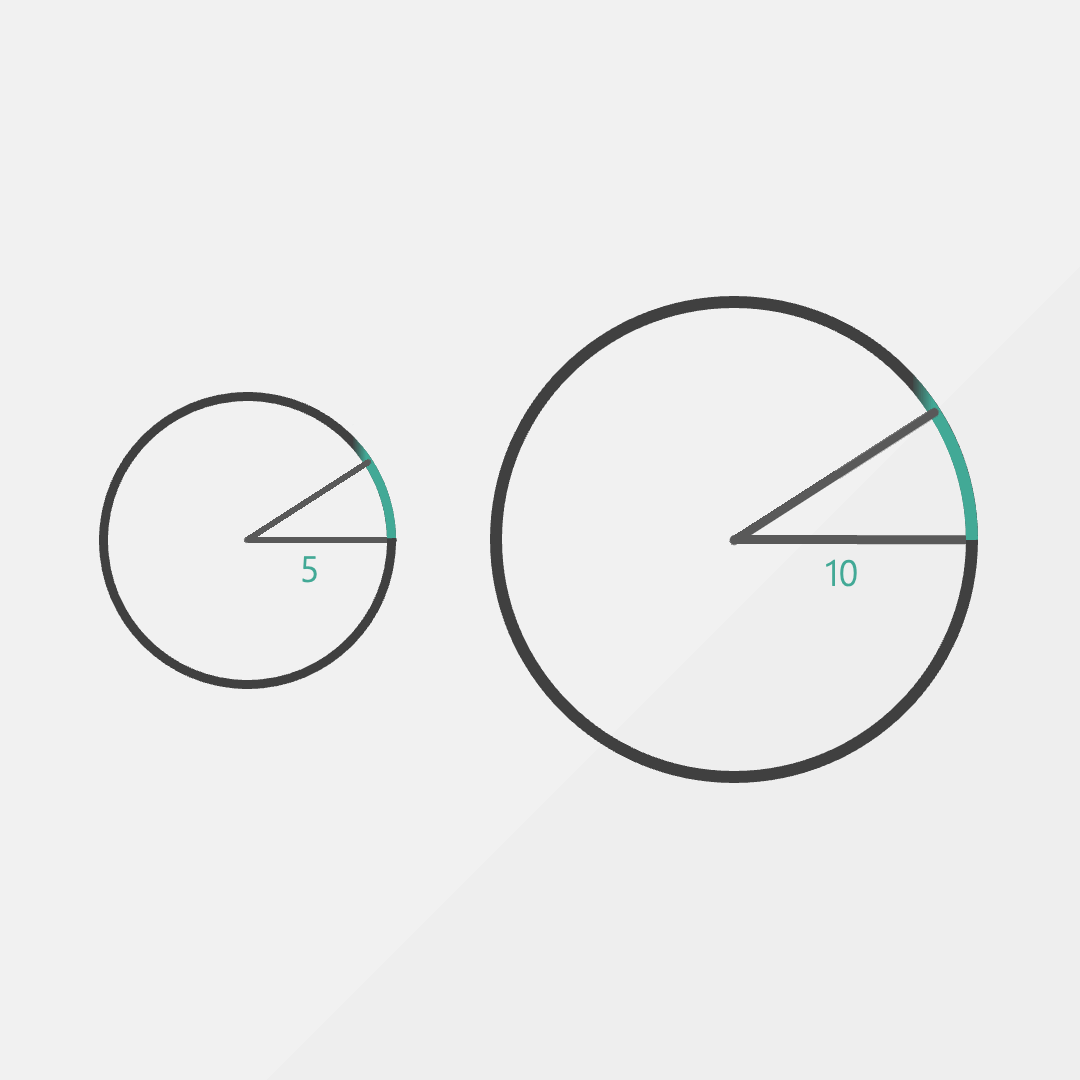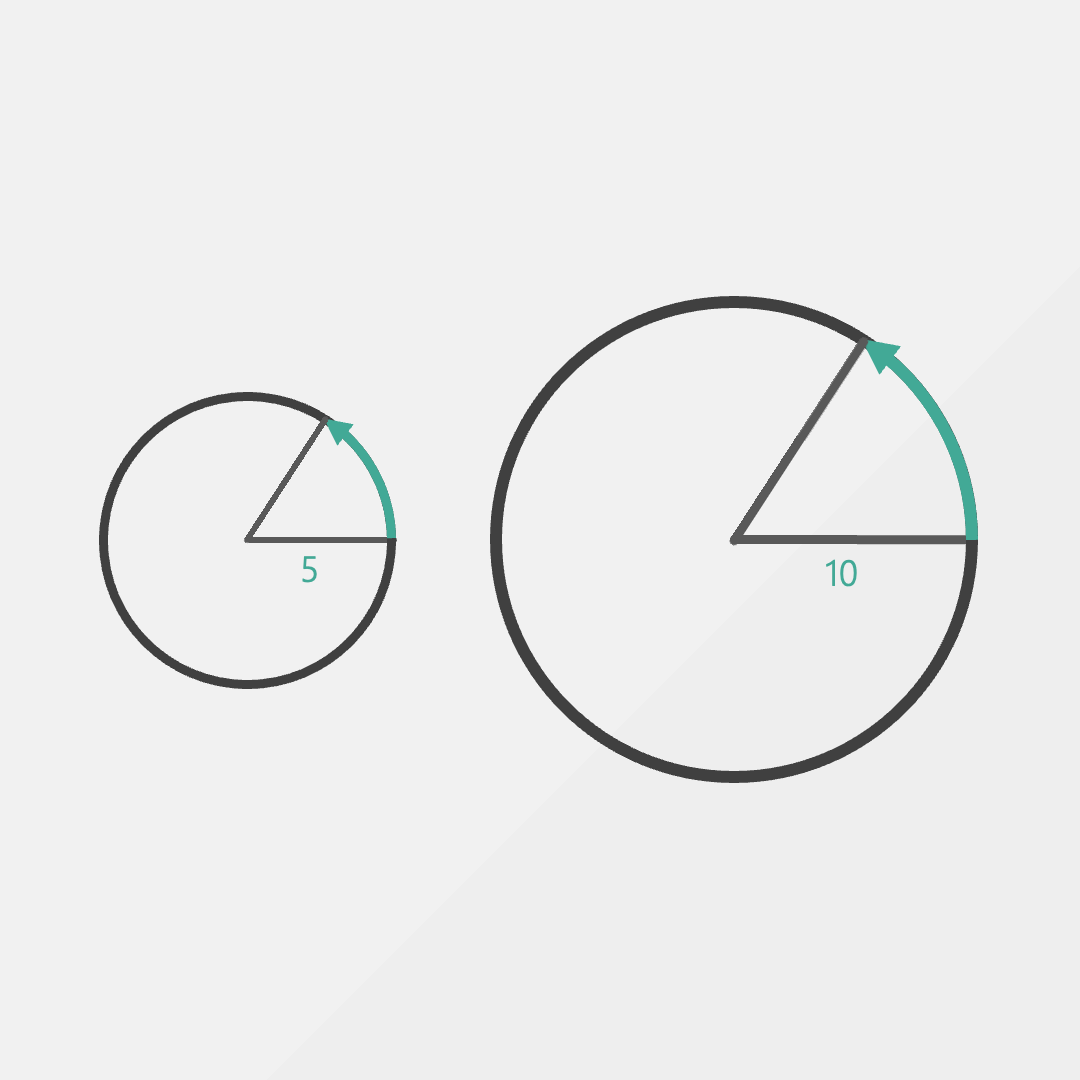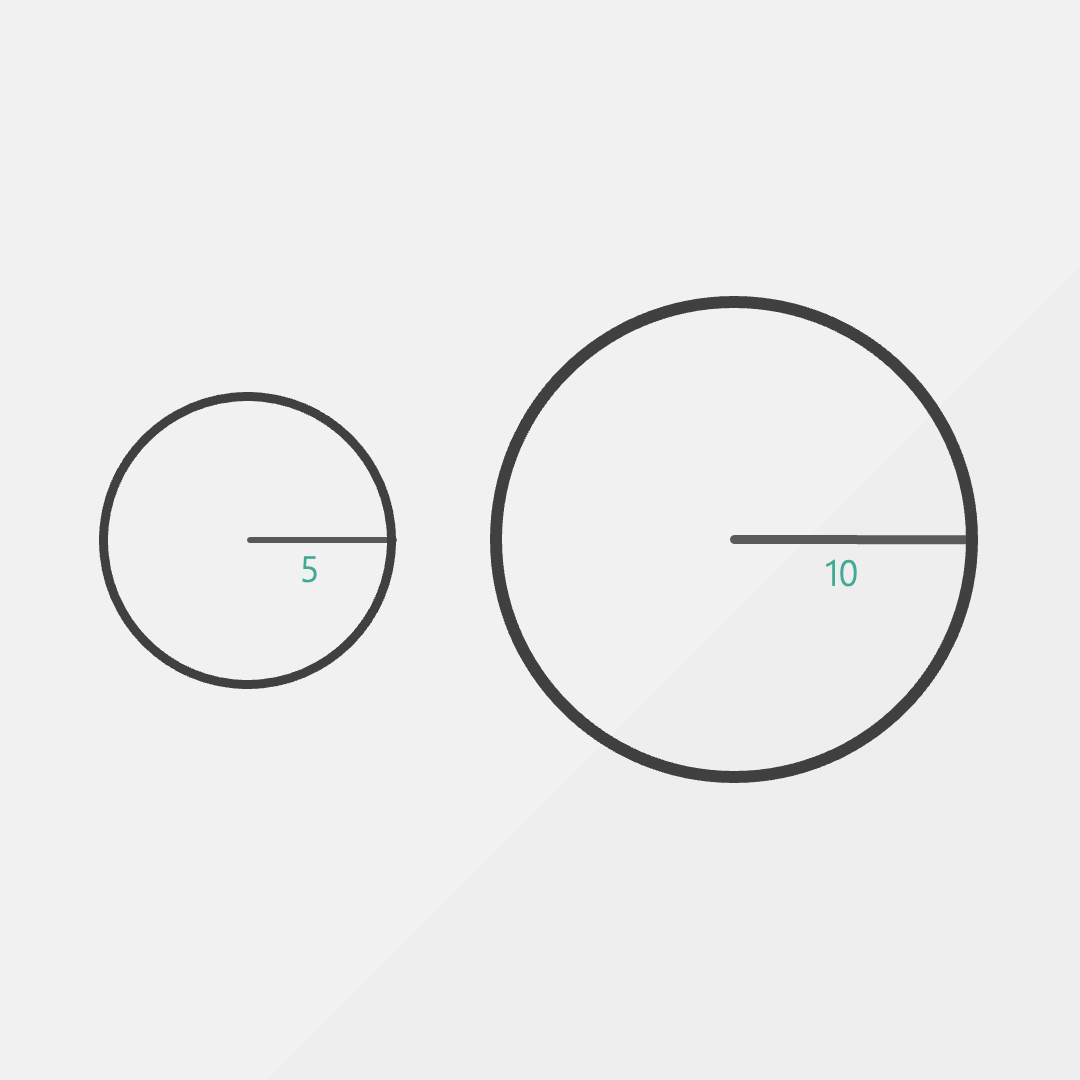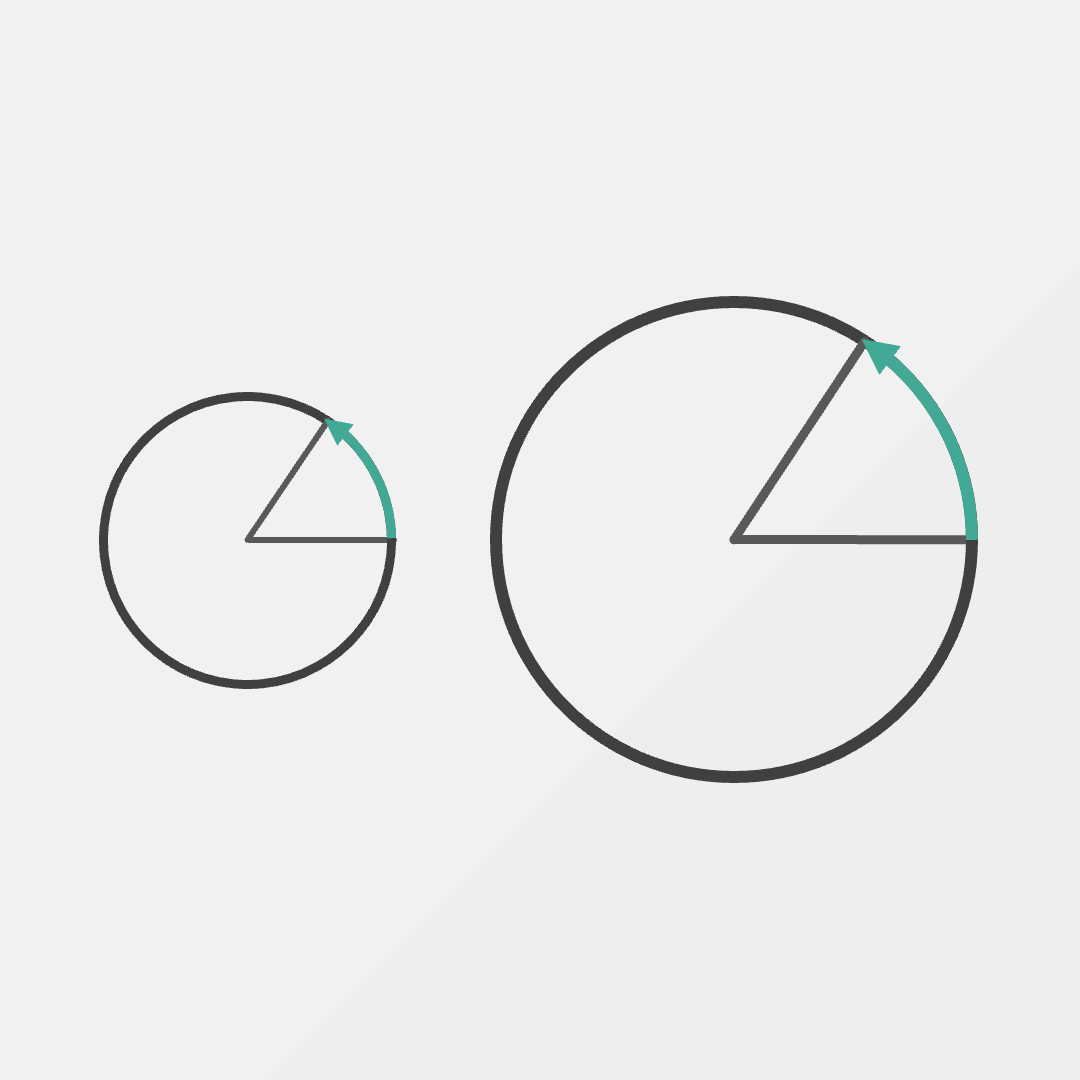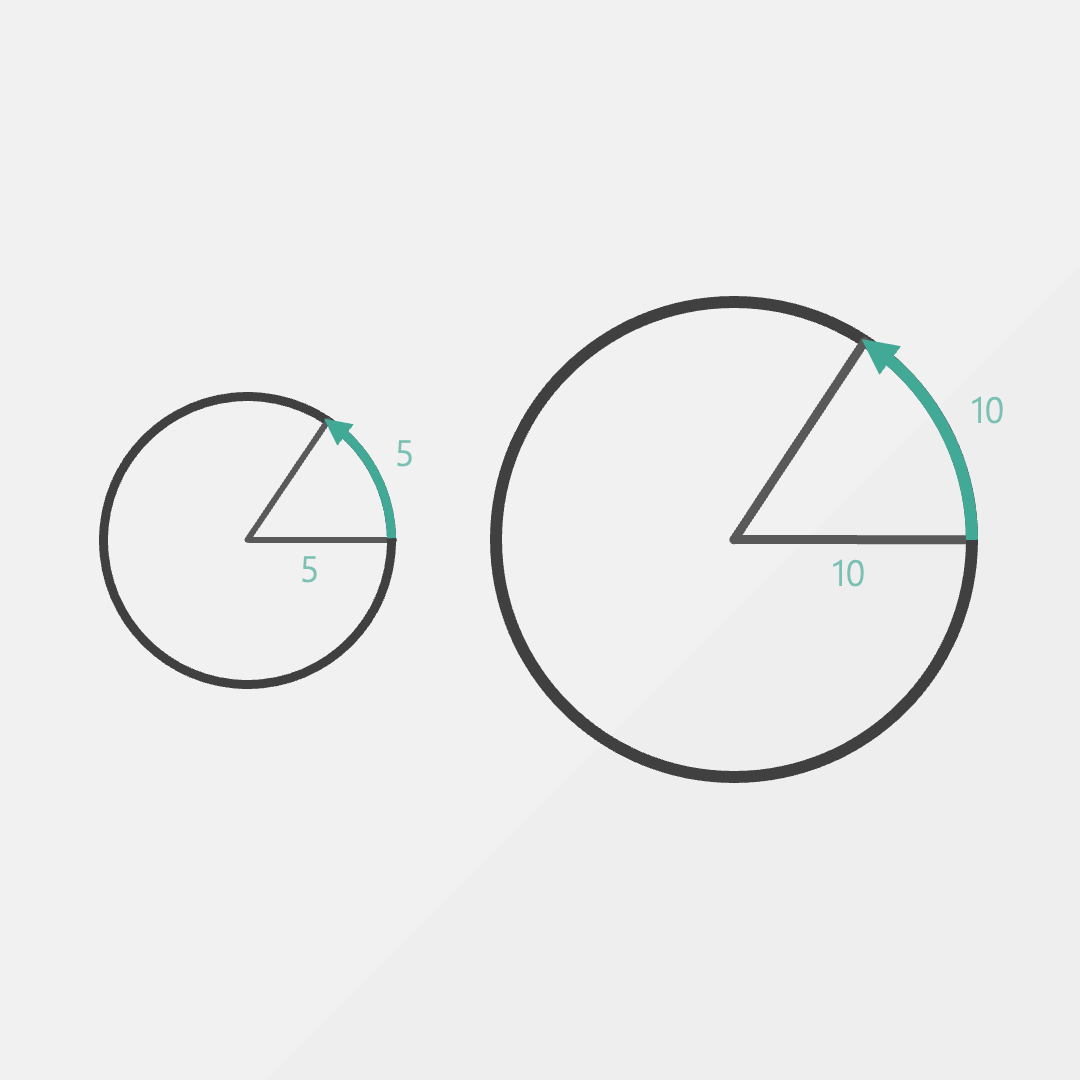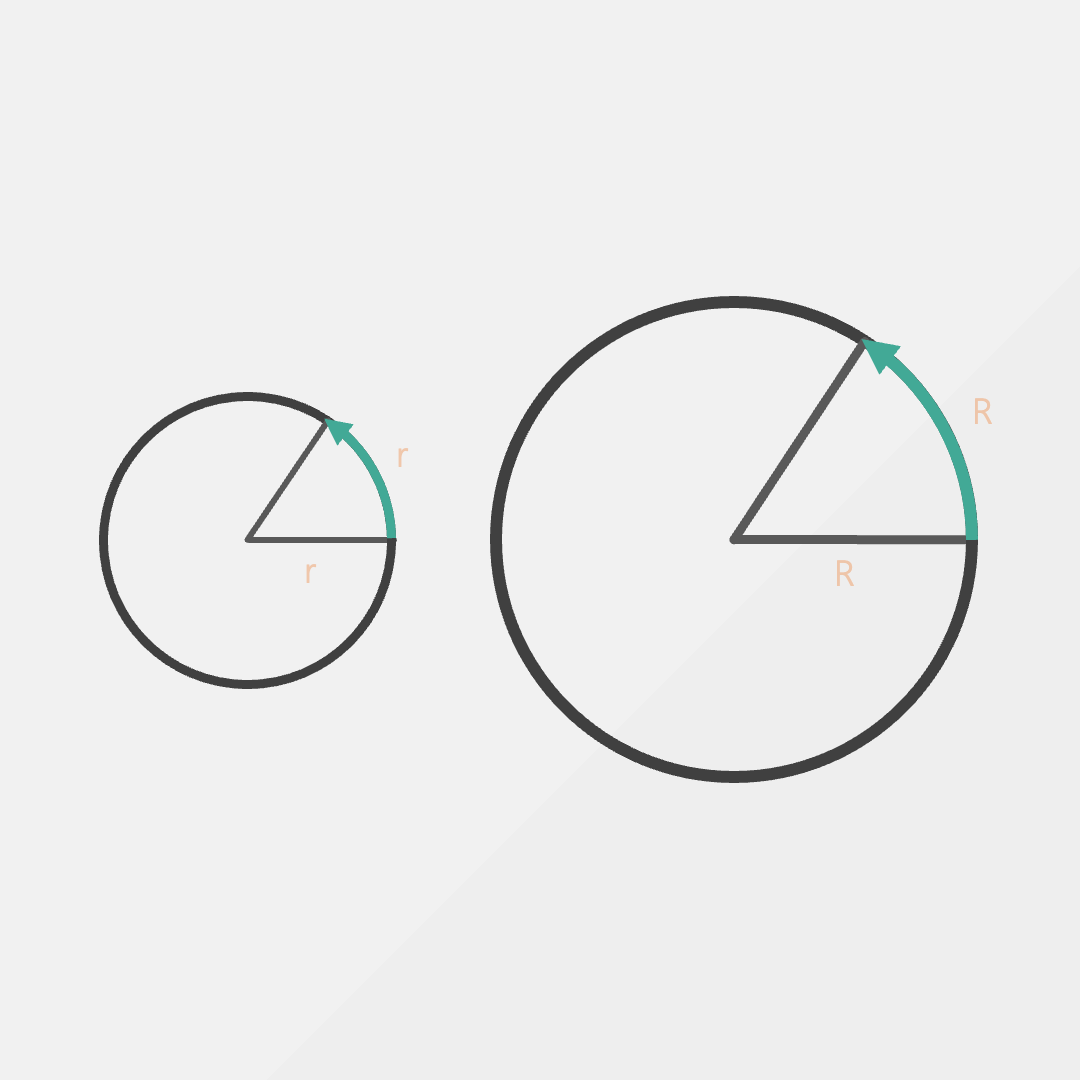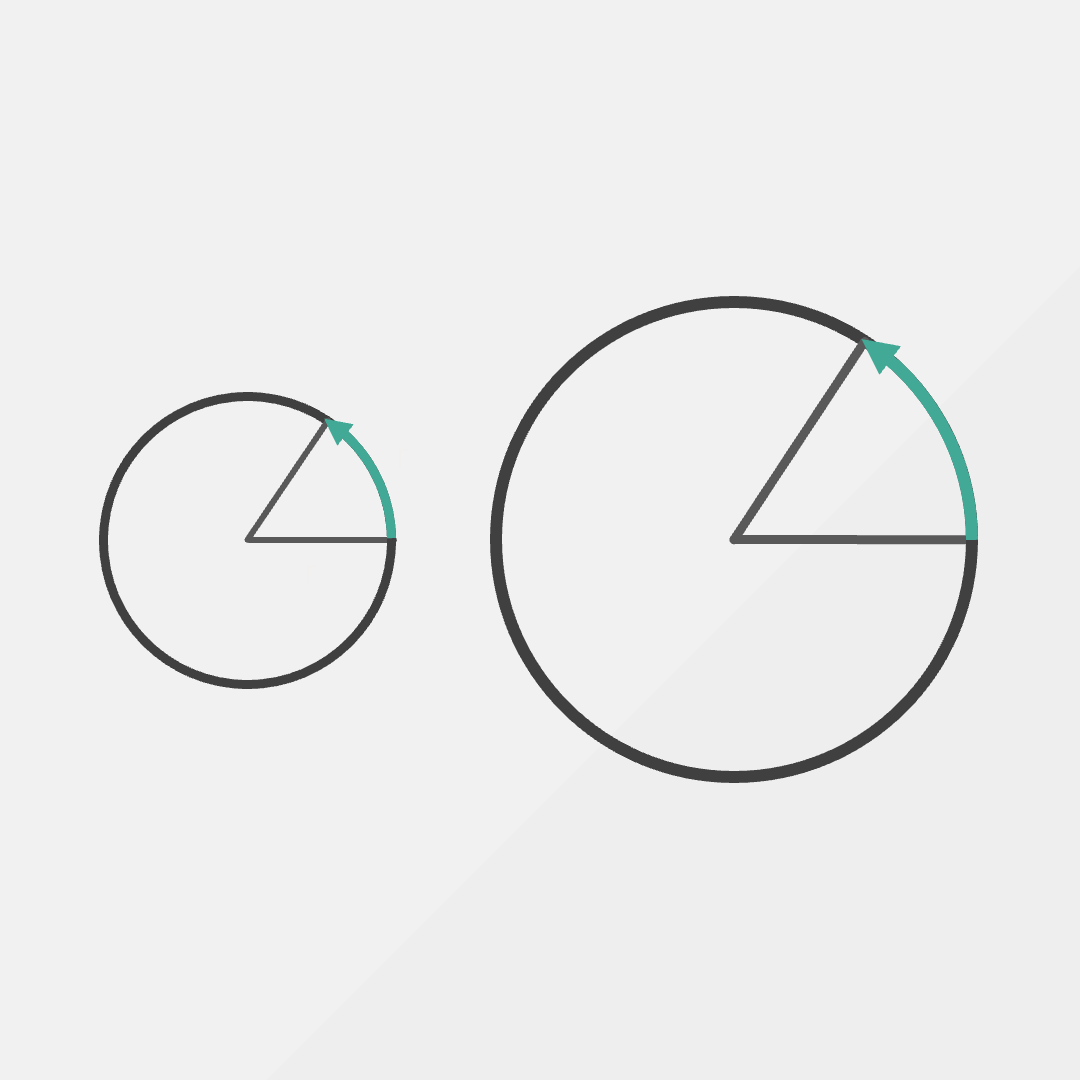Trig 00-01: Radians
Heads up
So we’re going to start off the radians section with a little heads up for the audience: radians are weird.
They do get much easier with practice but never get quite as easy as, say, degrees or turns. (Part of this is due to pi being defined incorrectly which we’ll discuss in the next lesson.)
I think for this reason, radians are often taught in the middle of a unit on Trigonometry so as not to scare away students right at the beginning. But, if you are learning trig in the classroom today, you will have to learn them sooner or later. In my opinion, it’s best to see them early and as frequently as possible. That way, even if you don’t like them, at least they will be easy to use.
The rest of trig is much simpler, trust me! If you feel overwhelmed by this topic, feel free to come back to it later. You can do all of Trig without ever learning what a radian is.
Hopefully one day, the world will switch over to tau and students will no longer have to deal with the disastrous combination of radians and pi.
Until then, I hope that this article and the accompanying review sheet makes the learning process a little bit easier.
Ok, in the last section we explored different ways of describing rotation, primarily degrees. In this section we will take a look at the second most popular system for measuring rotation, radians.
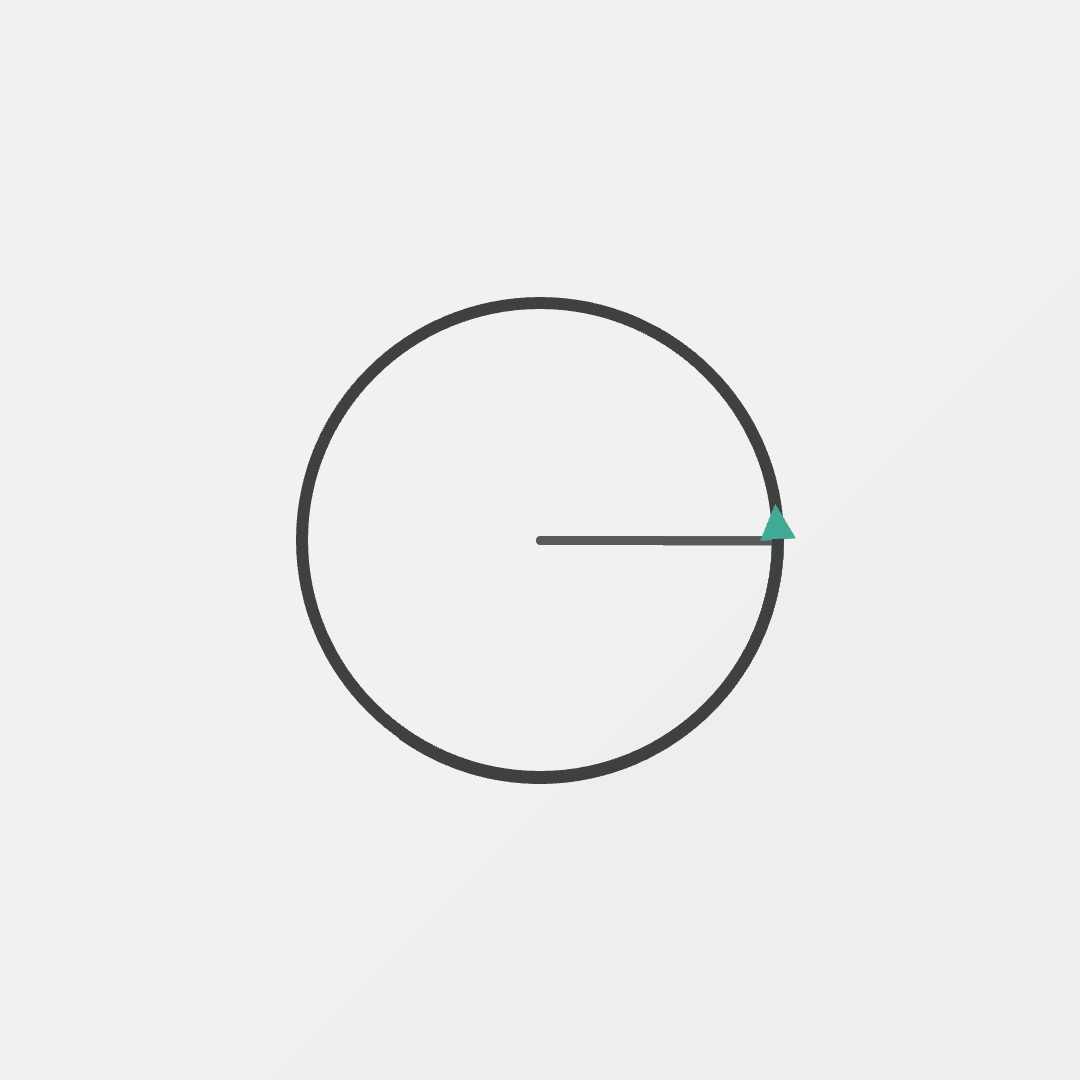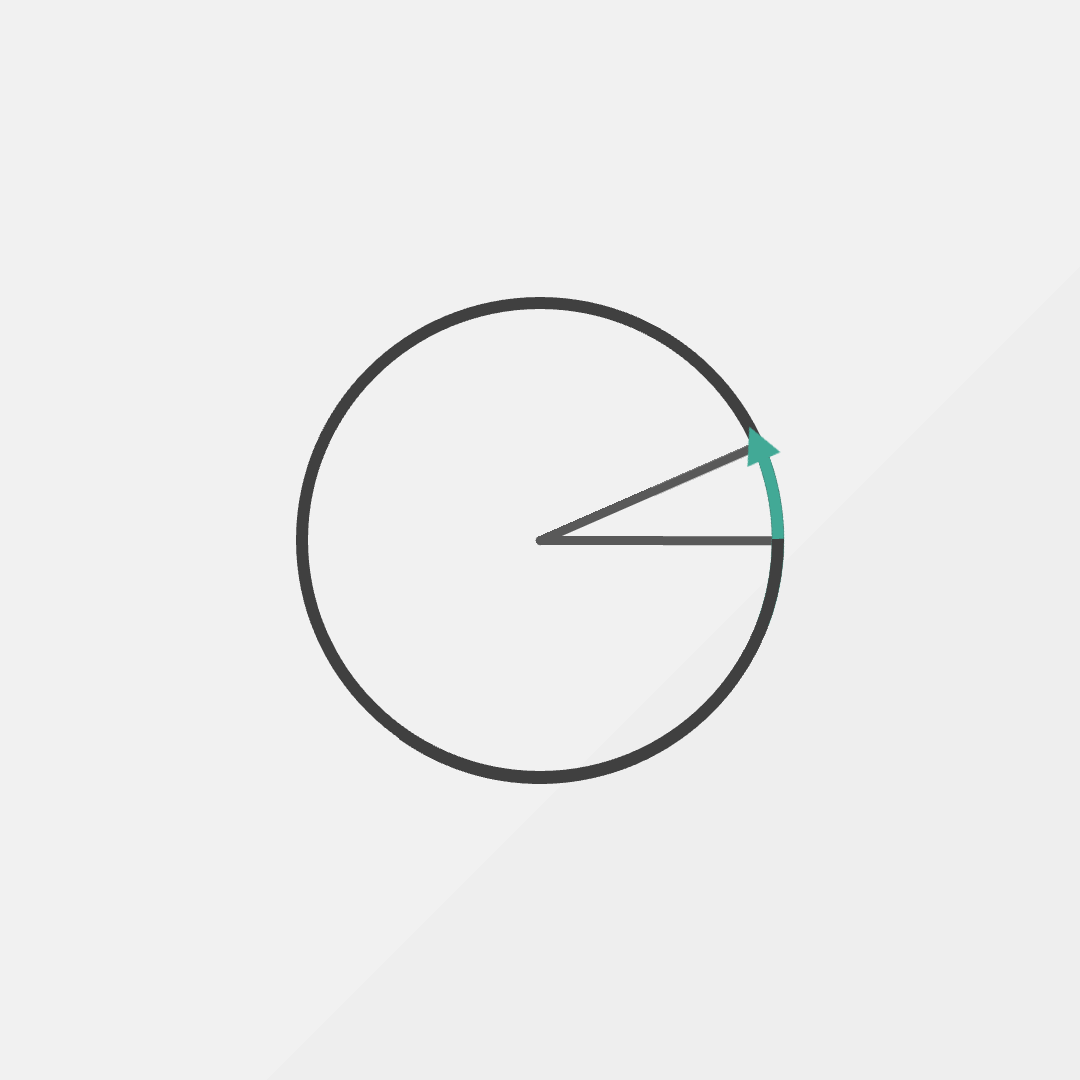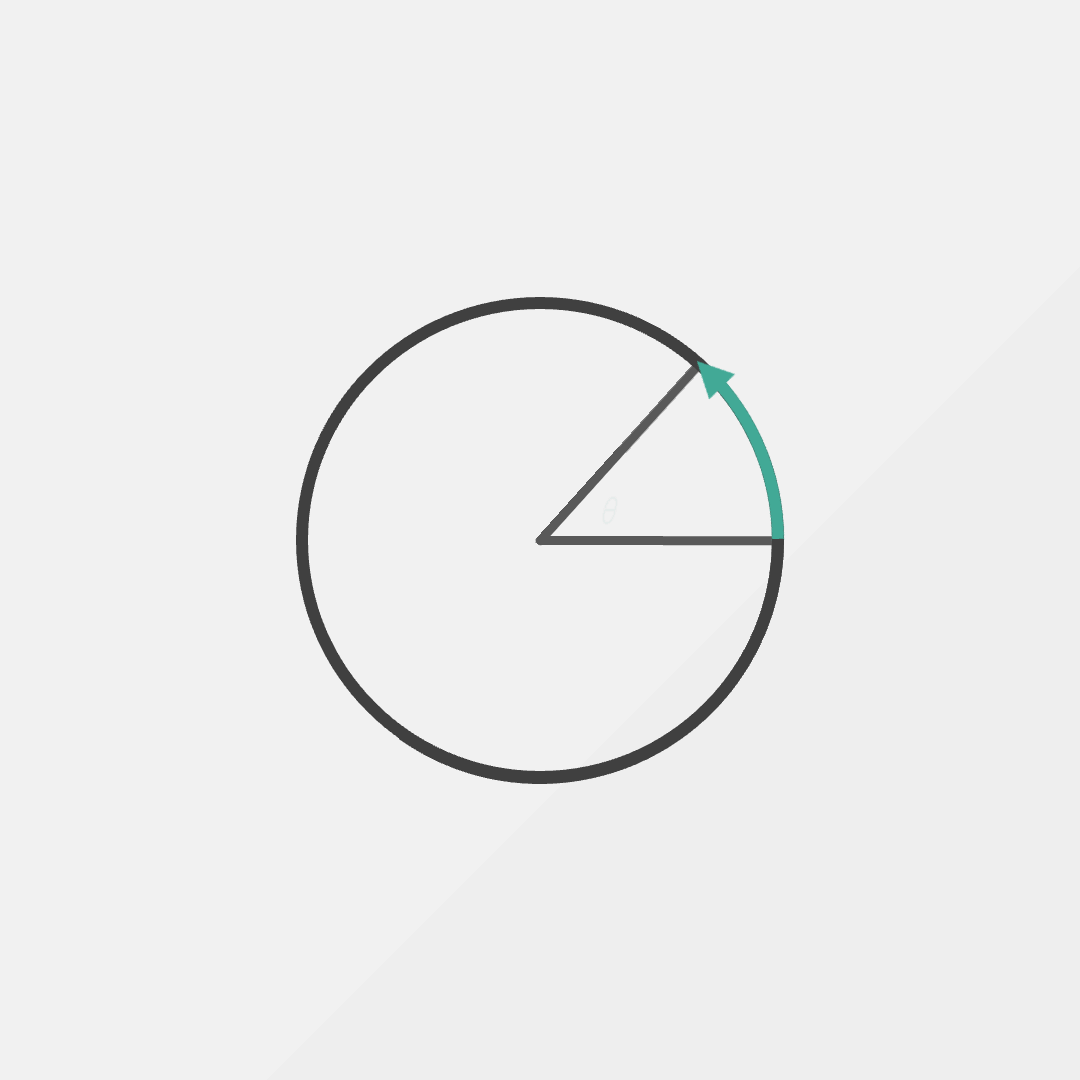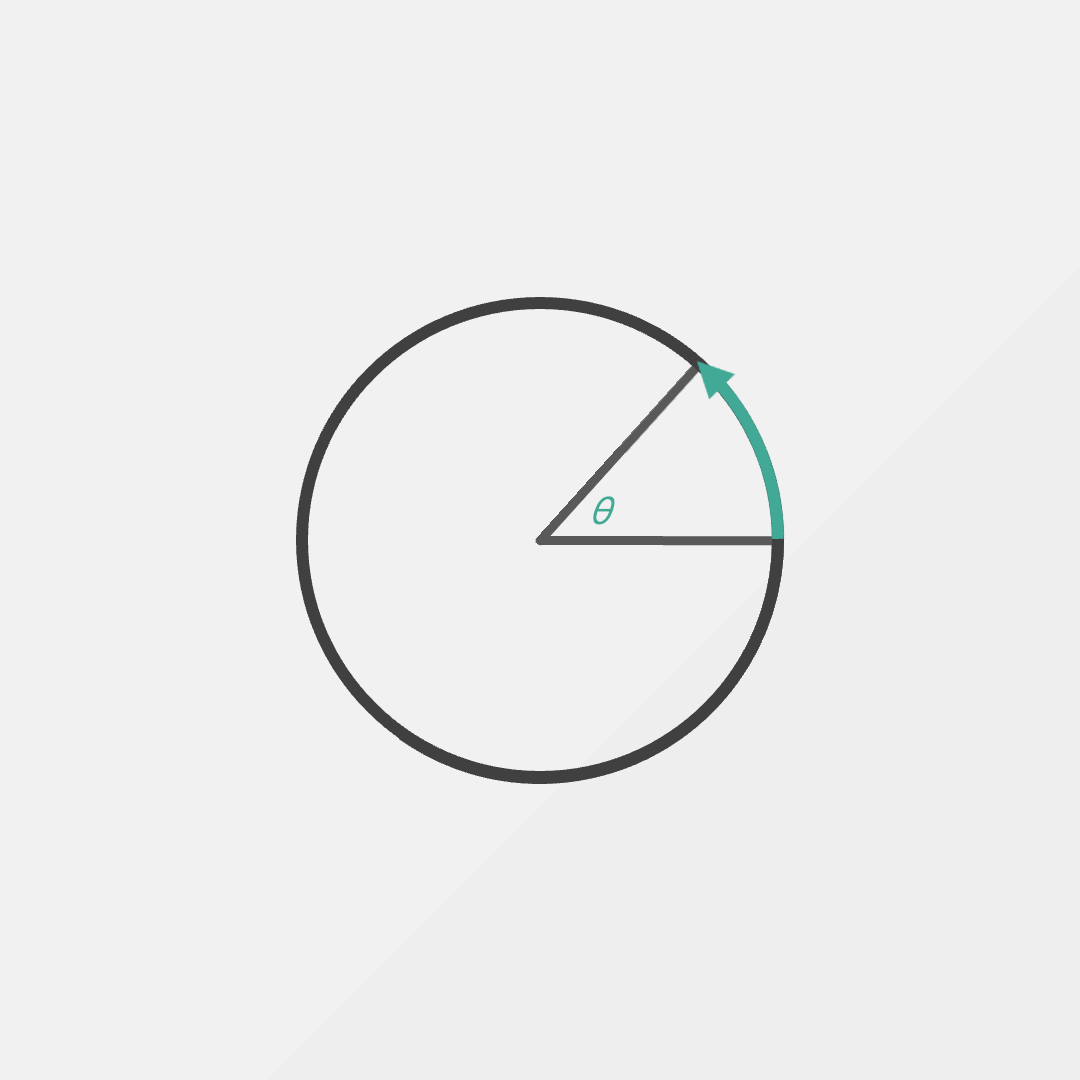
One way to think about rotation and angles is distance. Imagine standing on the edge of the circle shown and walking around counter-clockwise on the perimeter.
As you traverse this path, the distance traveled is actually linked to an angle.
Let’s say we have two circles, one of radius 5m and another of radius 10m. If we walked a distance of 20m, what would be the resulting angle?
Well, we can clearly see that the angle is completely different in both circles.
It wasn’t a terrible idea, but it turns out length isn’t a perfect way to measure rotation.
Fortunately, not all hope is lost. If we switch to thinking about distance in terms of the radius, we find that both angles are suddenly the same. In the smaller circle, we walk a distance of 5m and in the larger circle a distance of 10m.
It doesn’t look like much, but this is a radian. A radian is defined as walking one radius on the edge of the circle.
And just like that, we have a whole new way to talk about angles. What would 2 radians look like? Well we just walk a distance of two radius-es (ok, so the plural is actually radii) on the edge of the circle. What about 3 radians?
Can you work out how many radians there would be in a full turn?
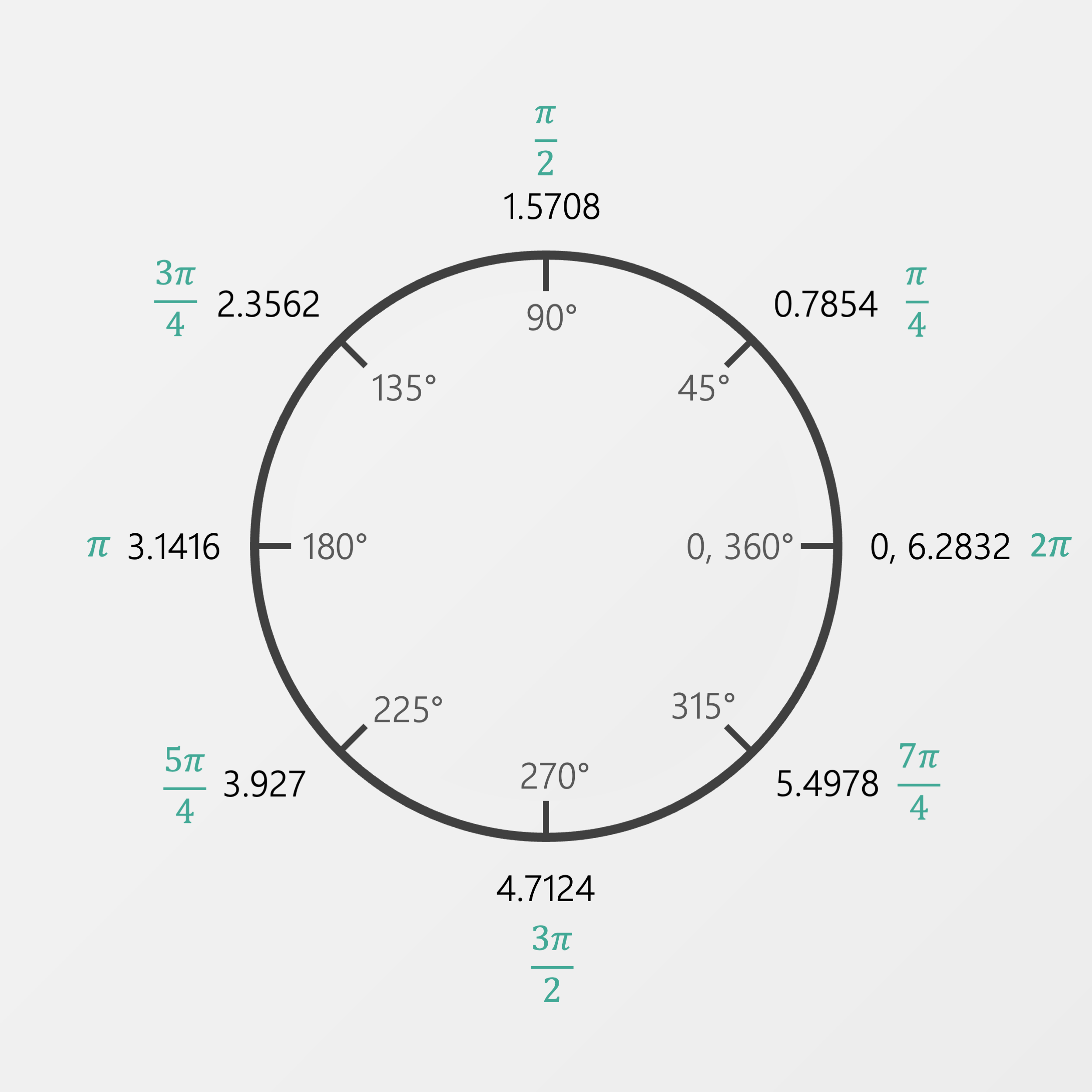
If 6.28 looks familiar, you might recognize this as 2𝜋.

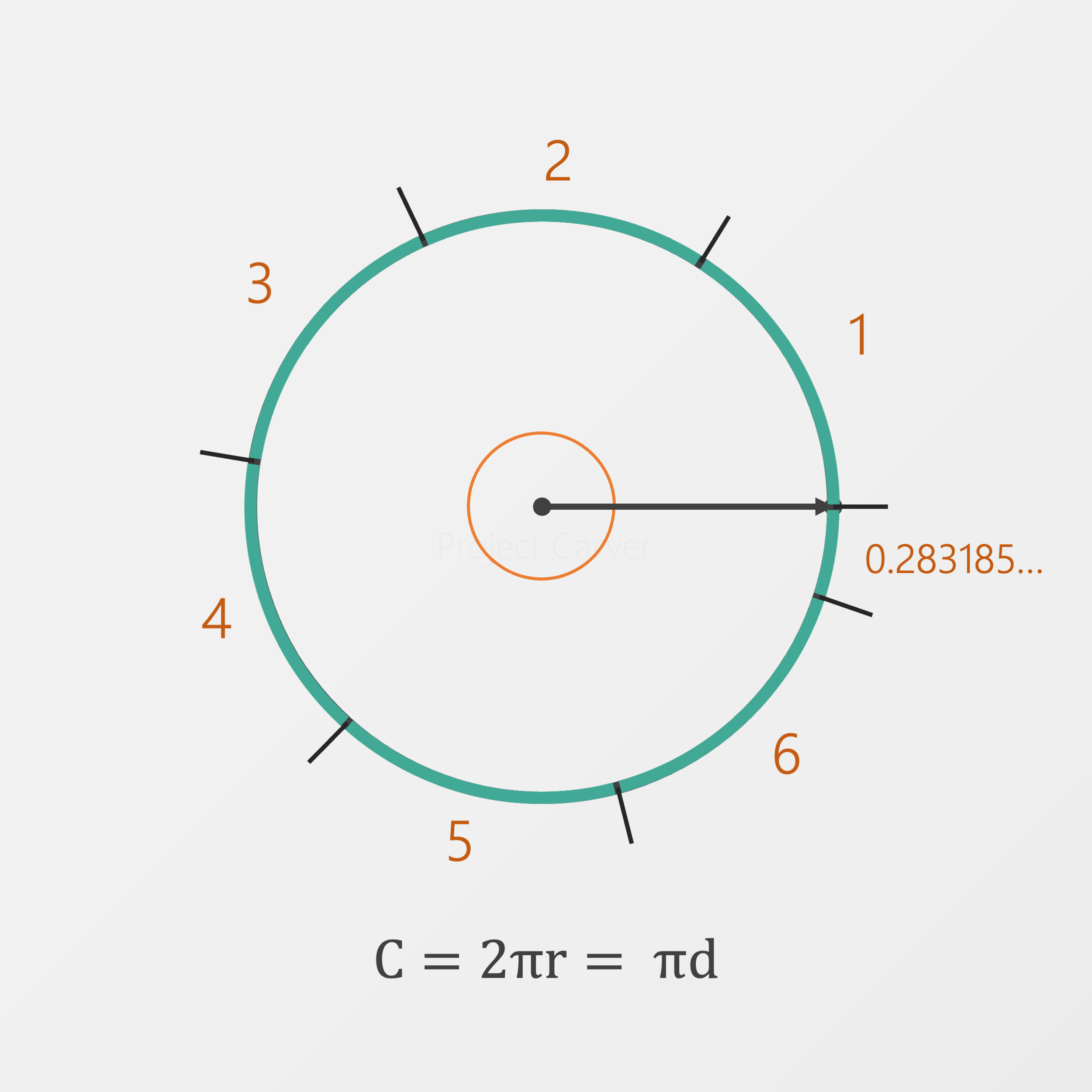
We can see that there are 6 whole entire radius-es and then one little 0.28 part. It’s not a super elegant number but that’s a full rotation in radians.
Ok, but what about some normal, actually useful, angles like a half-turn or 45 degrees? Let’s take a look at some of those.
All of these angles are pretty useful and show up very frequently. Can you work out what these angles would be in radians?
You might notice that the numbers once again are somewhat…non-ideal. A quarter-turn is π/2. It’s somewhat counter-intuitive. Radians can also be written as a decimal or in terms of π. There’s a lot to keep track of. Thankfully, you won’t have to master all of this content right away.
Perhaps less useful, but we can also convert from whole number angles in radians to degrees. How many degrees do you think there would be in 1 radian?
As we can see, radians and degrees are like apples and oranges. But, in a classroom, there’s a good chance you’ll need to be very familiar with both and be able to switch between the two systems. Let’s see how to do that.
No matter what system you’re working in, the one thing that stays constant is the ratio of your angle compared to a full rotation. In this example, we see that 90 degrees is just a quarter of a full circle. So, in radians, there is some angle measure that when compared to a full turn (2π) it will also result in a fraction of one quarter. You’ll need a bit of algebra to simplify and solve. You’re answer should come out to π/2.
Can you use the same method to convert 25 degrees to radians? How about converting 2 radians to degrees?
The great thing about this method is that converting from radians to degrees is just as easy. Draw out your picture, write down your ratios, and then solve for the unknown. If this is challenging to solve, you’ll need to brush up on your algebra, ratio, and fraction skills.
Answers: 25 degrees = 5π/36, 2 radians = 114.5916 degrees
And with that, you’re well on your way to mastering radians.
As we can see, the idea of radians isn’t too difficult but the numbers do get a bit messy. Whereas it’s easy to hold the idea of 360 degrees in our mind, thinking about a radian takes a bit more work. One of the things we can do is to offload the thinking from our brains onto paper.
Below, you’ll find a nice review sheet summarizing everything you’ll ever need to know about radians.
Click on the images to navigate to the downloads page.
Have some resources that make radians easier to learn? Share them down below in the comments.
Want to use these animations for a class? Head over to the animations downloads page. Custom animations are also available upon request.