Trig 00-03: Turns
I know. You’ve probably been wondering for the last two lessons: wouldn’t turns be so much easier? We’re already using them to convert from degrees to radians. We don’t have to deal with pi or tau. They’re simple and intuitive and there’s no new math to learn. How could radians possibly be better?
Let’s take a look at our diagrams from before, now with turns present.
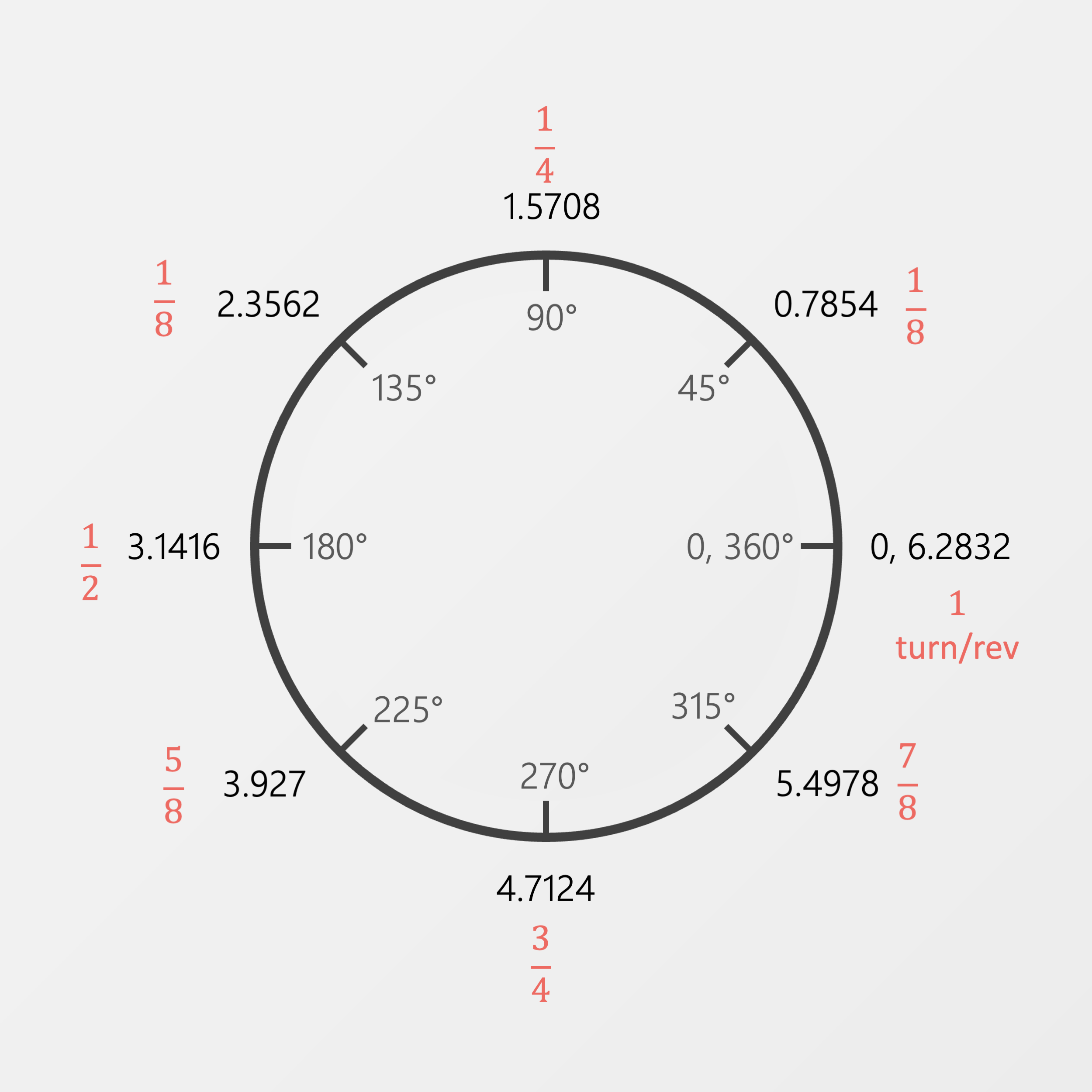
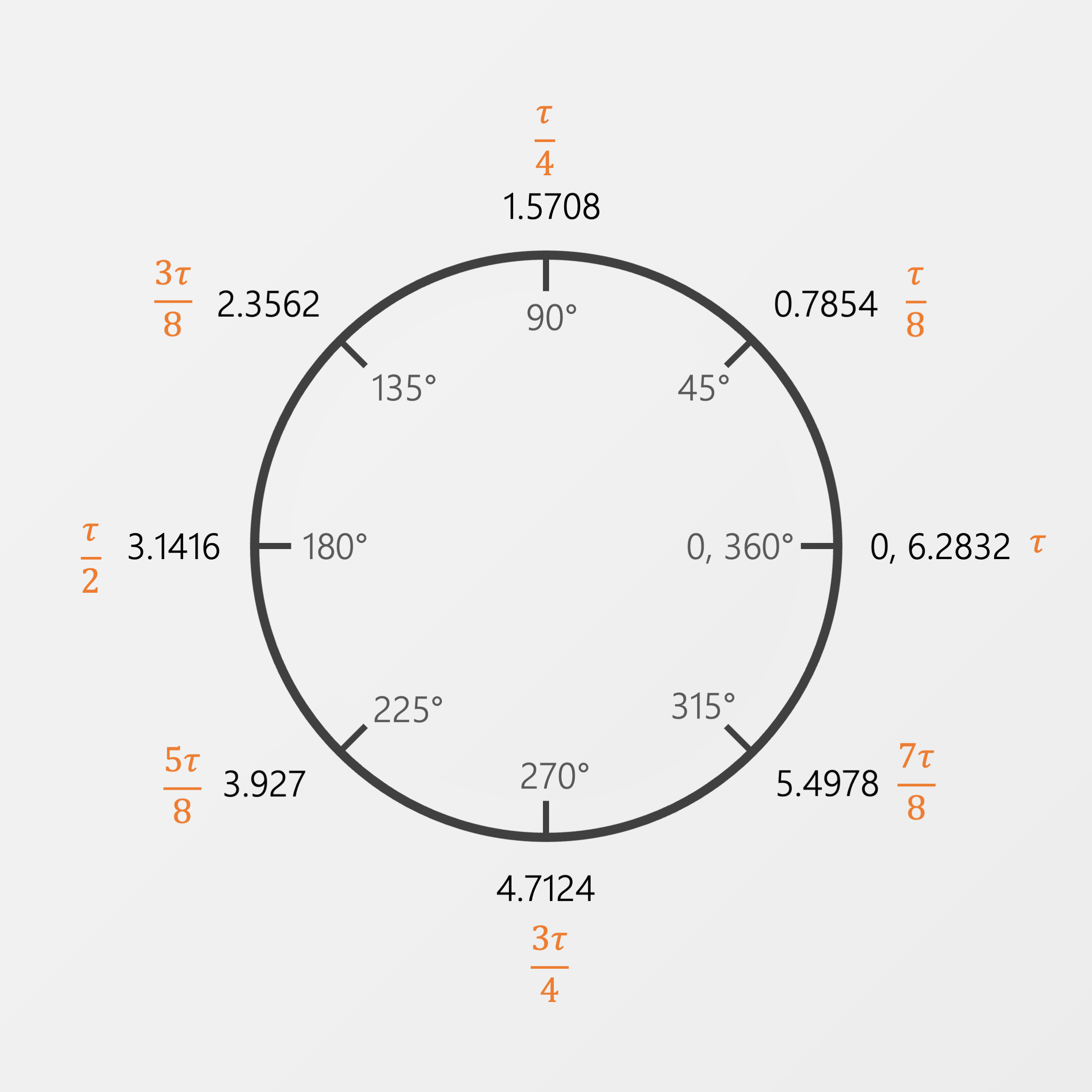
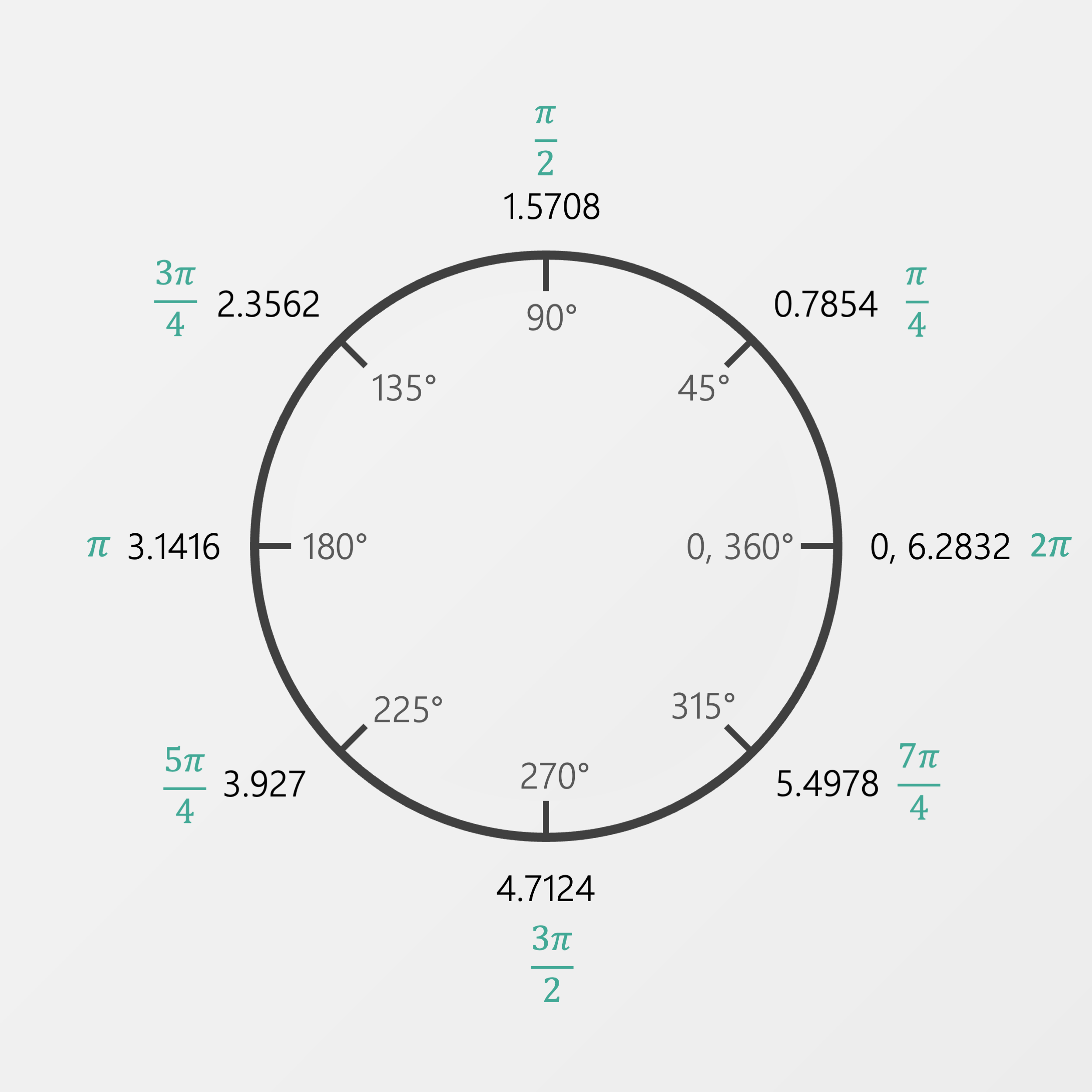
So much better. Surely this must be the best, most natural way to represent rotation? We only needed one paragraph to explain it.
But to answer that question, we need to take a step into the not too distant future.
Ok, this is the end of the discussion on turns. Everything below is the argument for why radians still win out.
We mentioned in lesson one that radians were important as soon as calculus. Let’s see if we can take a peak into the future and see why.
Below we have a graph of sin(x). We haven’t discussed this function yet (that’s the next lesson) but perhaps this graph already looks a bit familiar as the wave function (used to model things like light waves, radio waves, sound waves, etc.).
What we’ve done here is graph this function using four different systems of rotation (turns/revolutions, degrees, radians, and diamerians). The x-axis is the input angle and the y-axis is the output of sin(x). We’ve defaulted to radians for the x-axis.
There are two important things to take away from this graph:
is that sin(1 rad) and sin(1 turn) and sin (1°) and sin(1 dia) are very different values
is that the slopes of these functions are very different
While we might not know why these two things are important, we can hopefully feel that there’s something interesting happening at small values.
Let’s scale each of these outputs relative to the input.
\[ \frac{sin\ x}{x} \]
We arrive at a fundamental step for the derivative of the circle functions. Let’s take a look at the graph for this function, again for all four systems of rotation.
Any guesses what the values at zero are?
What we see near zero (also known as the limit as the angle approaches zero) is that each rotation system produces a constant.
\[ \frac{sin_{turns} \ ( 0)}{0} \ =\ 6.283185...\ =\ \tau \ =\ 2\pi \]
\[ \frac{sin_{diamerians} \ ( 0)}{0} \ =\ 2 \]
\[ \frac{sin_{radians} \ 0}{0} \ =\ 1 \]
\[ \frac{sin_{degrees} \ 0}{0} \ =\ \frac{6.283185...}{360° } \ =\ \frac{\tau }{360° } \ =\ \frac{2\pi }{360° } \]
Note: we’re not actually dividing by zero here but instead a really really really really small value (think 0.000000001)
Also if you’re skeptical that this happened only because our x-axis is in radians, try repeating this experiment with the graph set to degrees.
Hopefully each of these constants look familiar. They’re the converting fractions to convert from any rotation system into radians. It’s almost as if there is something natural about working in radians.
Once we start our study of calculus, anytime we use a system other than radians, these converting factors will show up in every single one of our calculations. So, even if at first it doesn’t seem like it, radians really do eventually make our math lives easier.
Calculus gets messy when we use other systems of rotation
Ok, here’s one more visualization to drive the point home.
Radians is the only system where the length of the curve in orange is the same value as the angle itself. So as the angle gets increasingly smaller, the green and orange values approach a 1:1 ratio.
Extra credit:
If you’re a calculus student, try taking the derivative of the sine function using first principles.
Final thoughts:
At the end of the day, a lot of math is simply convention (what humans have agreed upon) and so the “correctness” is very much what we decide it to be. What might become simpler in a Calculus class might makes things more difficult for say a computer (see Turns are Better than Radians).
But, if you’re learning mathematics in any modern classroom, radians will continue to be the de facto standard for the foreseeable future. Best to get started learning them as soon as possible.