Trig 00-01: Degrees
Welcome to Trigononometry
We’re going to start off this entire unit on trig with a pretty simple concept: rotation.
And we’ll build to that idea in this article by first discussing something even simpler, direction.
Imagine yourself located in the downtown area of a sprawling metropolis. If you’re anywhere on Earth, that’s probably going to mean roads and city blocks laid out perpendicular to each other as shown.
Right now, you’re located at 5th and Roosevelt (in red) and you’re making your way to Columbus and 8th (in green). In this scenario, finding our way from start to finish requires just four directions. A simple compass with North, South, East, and West will do.
Traversing one block at a time, we can navigate anywhere in the city by using sequential steps. One possible way of navigating to our destination is following a path of East, North, East, North, East, and finally North.
But, what about when we are located on streets that are not perpendicular? What if we find ourselves in the forest or navigating across an ocean?
It’s time to head out of the city and onto the open seas. We are currently located on the deck of a cargo ship in the Panama Canal. Our new destination is one of the busiest shipping ports in the world, the Port of Rotterdam (located in the beautiful Netherlands).
Out here on the boundless ocean, it becomes very clear very quickly that our compass of old is no longer going to cut it. We could have our ship travel East first until it is below Rotterdam and then travel north, but this clearly would not be a very efficient means of travel. (Not to mention, we would most likely crash into the coast of Africa long before reaching the Netherlands). We want a nice diagonal path straight to Rotterdam. We need more directions on our compass.
Much better. It looks like northeast is exactly what we need.
…or not. So we’re getting pretty close but setting a bearing for exactly northeast seems like it will send us crashing onto a UK coast somewhere. We could add some more directions to our compass but what would we call them? NEE? SWS? And that’s just for 16 directions. What if we wanted 32 or 100?
The naming gets pretty ridiculous pretty quickly and so we swap our names for numbers, like a good mathematician.
As we switch over to numbers, it brings another question. How many directions would be enough?
Mathematicians agreed on 360 as a pretty useful number (we’ll get to the why in a moment). If we think about 360 directions equally spaced around our circle with number 0 at due east, then NE falls right on the 45th direction (assuming we count counter-clockwise).
Most students will have had experience with degrees since elementary school. If it’s been awhile since you’ve worked with degrees, a quick internet search will get you up to speed in no time (maybe read the section below first before you do).
By adjusting our initial bearing from 45 to 40 degrees, our ship heads right where its needed.
We’re still getting to our discussion of 360 and degrees, but we’ll say one more thing. 360 is a pretty big number, but if we imagine an even bigger scenario, say….I don’t know, space travel? Would degrees still work?
Our cargo ship is now a rocket ship traveling from Earth to the Moon. It’s an oversimplification, but we’ll once again assume our spaceship can also only set its trajectory once and travel in a straight path. In this scenario, 360 directions isn’t enough.
Adjusting our trajectory by just 1 degree would mean missing the Moon by almost two whole moons. That’s being off by 6710 kilometers or 4169 miles.
Let’s recap:
Over the first half of this lesson, we’ve established two things:
Direction is important in a lot of scenarios
Our system of measuring has to accommodate the small and the large
Ok, we’re finally ready to talk about degrees.
We’re going to start off with a circle. As we saw previously, if we have an infinite number of directions, we end up with a circle where we can turn in any direction. Let’s put our angle from before back in.
Try it out
If you have some free time, take a moment to come up with some ways of describing this angle. Is your solution simple? Complex? Does it allow for measuring big and small changes? Does it work better than degrees and radians?
Alright, on to the topic of degrees.
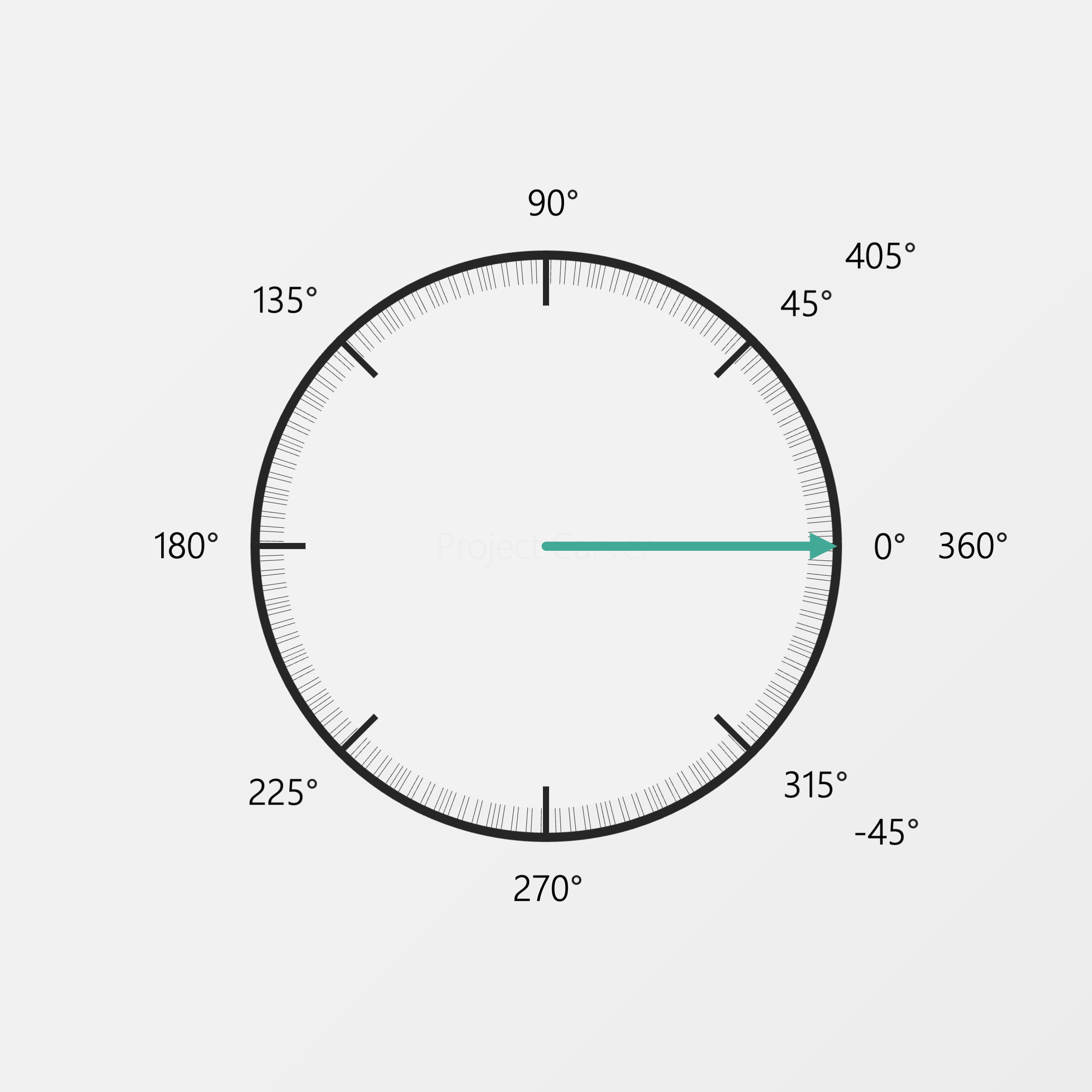
In the degree system, we start at the right and move counter-clockwise until we come back to our starting position. You’ll notice in the animation that there are angles bigger than 360. For example, 405 is the same as 45.
(You might have also noticed we’ve switched from talking about directions to discussing rotation now. Rotation is just a change in direction.)
Now, there’s no reason to go counter-clockwise. In other areas, such as navigation in planes and ships (called a bearing), the turn starts at the top and goes clockwise.
In math, if you go clockwise, that is considered a negative angle.
This is a pretty great system and the precision can even be increased by using decimals. Overshooting the moon is no longer a problem.
You might still be wondering though, why 360?
It turns out there isn’t really anything special about 360. We could divide our circle into 100 parts, 400 parts, or any number really.
Try it out
Try a few numbers of your own. What do you notice? Do some numbers work better than others?
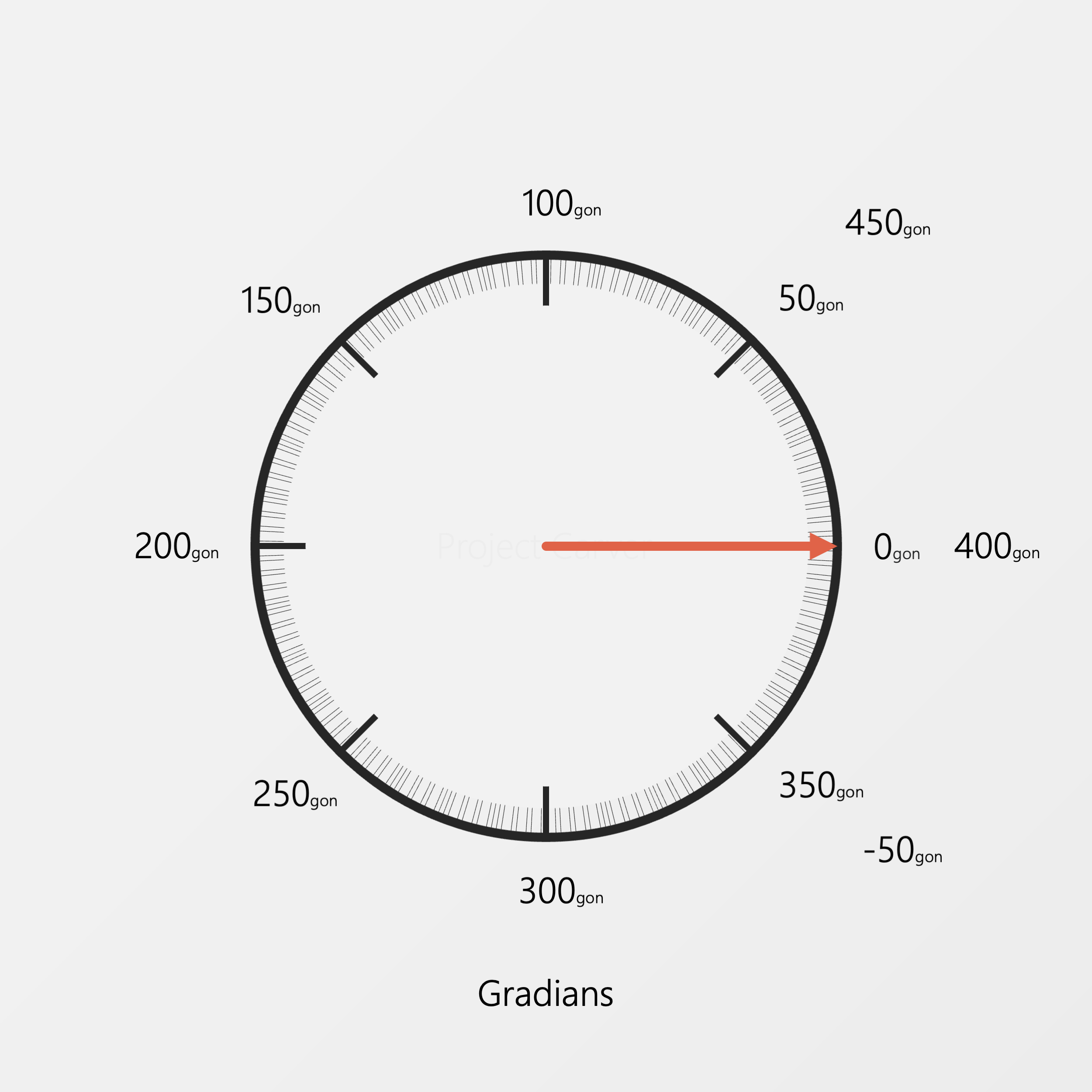
When we divide our circle into 400 parts, this is called the Gradian system.
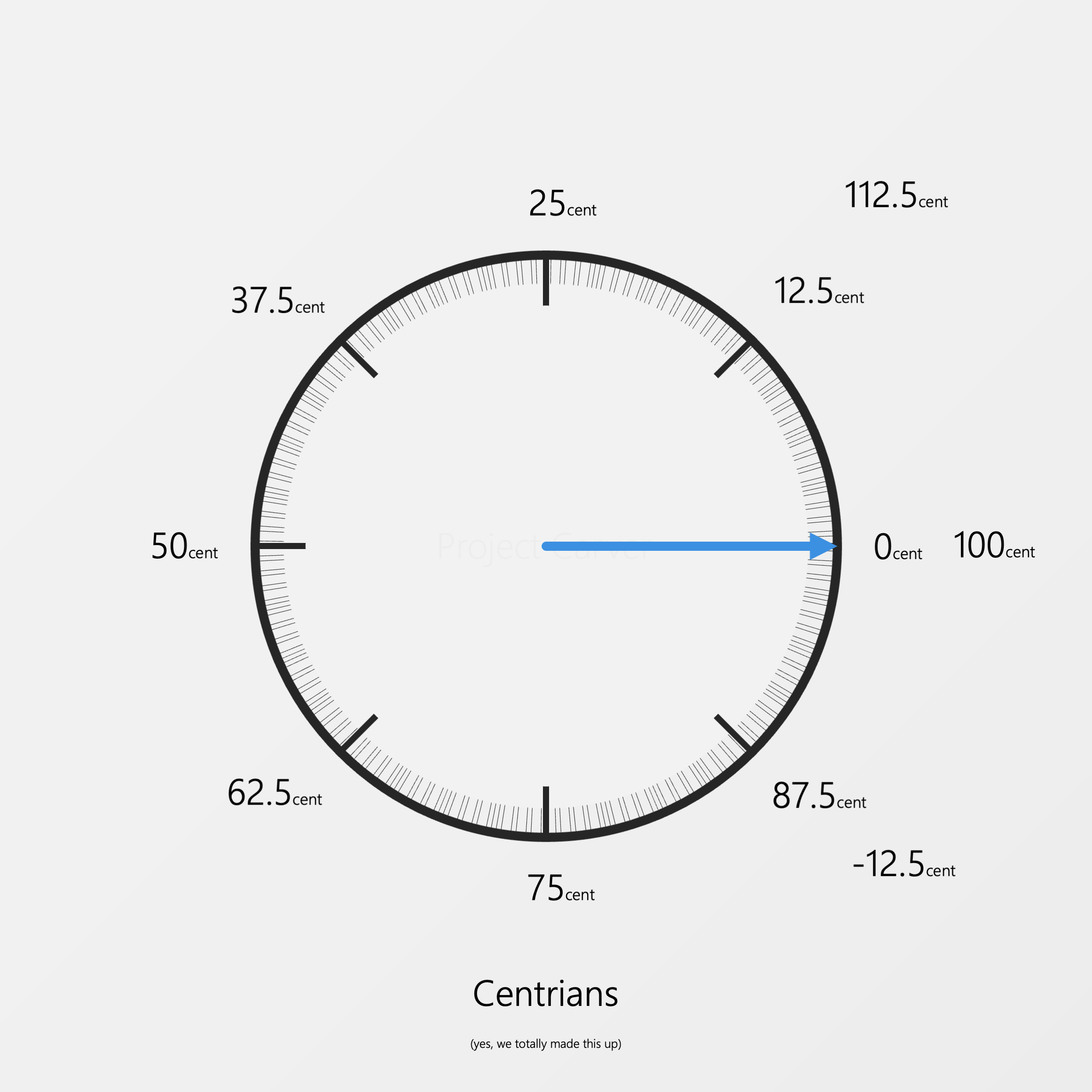
We could even make up our own system called Centrians where the circle is divided into 100 parts.
Notice anything interesting?
It turns out that 360 is actually a pretty great number. A lot of common angles like a half-turn or quarter-turn have nice whole numbers.
Further exploration
The origins of 360 and how it became popular are still somewhat unknown. For more math exploration, also make sure to check out other systems that are currently being used or have been used throughout history like turns and milliradians.
At the end of the day, 360 is still just an arbitrary number that mathematicians picked out. It’s not a problem now, but as soon as Calculus, degrees stop working so well. That means we have to switch over to a new way of thinking about rotation sooner or later.
Even though we won’t need it until Calculus, most classes will start teaching the new system much earlier than that.
So to keep up with everyone else, in the next section we are going to learn about radians.
Want to use these animations for a class? Head over to the animations downloads page. Custom animations are also available upon request.